Formule statistique de test standardisée

Si vous passez le test de statistiques AP, vous devez connaître la formule générale d’une statistique de test standardisée. Les statistiques de test standardisées sont utilisées dans les tests d’hypothèse. La formule générale est:

Statistique de test standardisée: (paramètre statistique) / (écart type de la statistique).

La formule en elle-même ne signifie pas grand-chose, à moins que vous ne connaissiez également les trois formes principales de l’équation pour les scores z et les scores t.

Regardez la vidéo pour un aperçu:

Vous ne pouvez pas voir la vidéo? Cliquez ici.

Comment utiliser ces formules: Toutes les formules nécessitent que vous insériez trois informations:

1. Votre statistique de test. Par exemple, la médiane.
2. Le paramètre de population connu.
3. L’écart type de la statistique.

Statistique de test standardisée pour les scores z

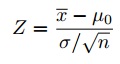
Pour des étapes faciles sur la façon de résoudre cette formule, voir: Comment calculer un score z.

Score T (population unique)

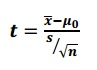
Pour des étapes faciles sur la façon de résoudre cette formule, voir: Qu’est-ce qu’une formule de score T?

Score T (deux populations)

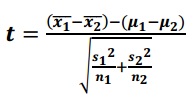
Que signifie une statistique de test normalisée?

Les statistiques de test standardisées vous permettent de comparer vos résultats à une population « normale ». Les scores Z et les scores t sont très similaires, bien que la distribution t soit un peu plus courte et plus grasse que la distribution normale. Ils font tous les deux la même chose. Dans les statistiques élémentaires, vous commencerez par utiliser un score z. Au fur et à mesure que vous progressez, vous utiliserez des scores t pour les petites populations. En général, vous devez connaître l’écart-type de votre population et la taille de l’échantillon doit être supérieure à 30 pour pouvoir utiliser un score z. Sinon, utilisez un score t. Voir : Score T vs score z.

Calcul d’une statistique de test standardisée: Exemple de problème

Besoin d’aide pour une question de devoirs? Consultez notre page de tutorat!

La durée de vie moyenne d’une batterie particulière est de 75 heures. Un échantillon de 9 ampoules est choisi et a un écart type de 10 heures et une moyenne de 80 heures. Trouvez la statistique de test standardisée.

L’écart type de la population n’est pas connu, je vais donc utiliser la formule du score t.

Étape 1: Branchez les informations dans la formule et résolvez:
x = moyenne de l’échantillon = 80
μ0 = moyenne de la population = 75
s = écart type de l’échantillon = 10
n = taille de l’échantillon = 9

t = 80-75 / (10/√9) = 1.5.

Cela signifie que la statistique de test standardisée (dans ce cas, le score t) est de 1,5.

Consultez notre chaîne YouTube pour plus d’aide et de conseils sur les statistiques!

Everitt, B.S.; Skrondal, A. (2010), Le dictionnaire de statistique de Cambridge, Cambridge University Press.
Gonick, L. (1993). Le Guide de dessin animé sur les statistiques. HarperPerennial.

—————————————————————————

Besoin d’aide pour une question de devoirs ou de test? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites!