mikä on Monte Carlo simulaatio?

Monte Carlon simulaatio on prosessi, jossa todennäköisyyskäyriä käytetään tuloksen todennäköisyyden määrittämiseen. Voit raapia päätäsi ja sanoa… ”Hei Rick, jakaumakäyrällä on joukko arvoja. Miten päätän lopputuloksen todennäköisyyden?”Ja mikä vielä parempaa, miten teen sen Microsoft Excelissä ilman erityisiä lisäosia, joita et koskaan kysyisi.Tämä tapahtuu ajamalla simulaatio tuhansia kertoja ja analysoimalla tuotoksen jakautumista. Tämä on erityisen tärkeää, kun analysoit useiden toisiinsa syöttävien jakelukäyrien ulostuloa.Esimerkki:

• # myytyjen yksiköiden jakaumakäyrä voi olla
• kerrottuna markkinahinnalla, jossa voi olla toinen jakaumakäyrä
• vähennettynä muuttuvilla palkoilla, joissa on toinen käyrä
• jne., jne.

kun kaikki nämä jakaumat sekoittuvat keskenään, lähtö voi olla melko monimutkainen. Tuhansien iteraatioiden (tai simulaatioiden) suorittaminen näistä käyristä voi antaa sinulle joitakin oivalluksia. Tämä on erityisen hyödyllistä analysoitaessa mahdollisia riskejä päätökseen.

Describe Monte Carlo

kuvaillessani Monte Carlo-simulaatiota viittaan usein 1980-luvun elokuvaan War Games, jossa nuori Mathew Broderick (ennen Ferris Buelleria) on hakkeri, joka käyttää soittamaansa modeemia murtautuakseen Pentagonin tietokoneisiin ja aloittaakseen 3.maailmansodan. Tavallaan. Sitten hän antoi Pentagonin tietokoneiden tehdä monia simulaatioita peleistä Tic Tac Toe opettaakseen tietokoneelle, että kukaan ei halua ydinsotaa-ja pelastaa samalla maailman.Kiitos, Ferris. Olet sankari.Tässä vilaus elokuvan näyttää big time Monte Carlo toiminnassa. Oletan, että sivuutat politiikan, kömpelön miehen halailun ja tietenkin Dabney Colemanin.

Jakaumakäyrät

on olemassa erilaisia jakaumakäyriä, joiden avulla voit tehdä Monte Carlo-simulaation. Ja nämä käyrät voidaan vaihtaa muuttujan perusteella. Microsoftilla ei ole valikkopalkissa ”Do Monte Carlo Simulation” – nimistä kaavaa:)

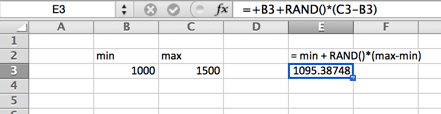
yhtenäinen jakauma

yhtenäisessä jakaumassa on yhtä suuri todennäköisyys missä tahansa minimin ja maksimin välillä. Yhtenäinen jakauma näyttää suorakulmiolta.

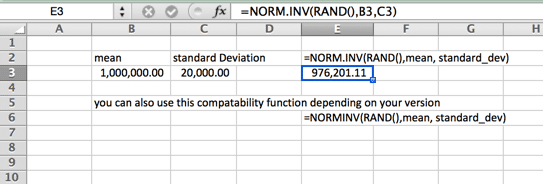
normaali (Gaussin) jakauma

tämä on myös normaali kellonmuotoinen käyrä. Tälle Monte Carlon Simulaatiokaavalle on ominaista, että se jakautuu tasaisesti molemmille puolille (mediaani ja keskiarvo ovat samat – eikä vinoutta). Käyrän hännät jatkavat äärettömyyteen. Tämä ei siis välttämättä ole ihanteellinen käyrä asuntojen hintoihin, joissa muutama yläpään talo nostaa keskiarvoa (keskiarvoa) reilusti yli mediaanin, tai tapauksissa, joissa on kova minimi tai maksimi. Esimerkkinä tästä voi olla oman paikkakuntasi minimipalkka. Huomaa, että funktion nimi vaihtelee versiosi mukaan.

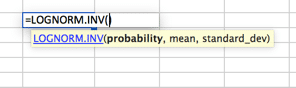
Lognormaalinen jakauma

jakauma, jossa logaritmi on normaalisti jakautunut keskiarvolla ja keskihajonnalla. Asetelma on siis samanlainen kuin normaalijakauma, mutta huomaa, että keskiarvon ja standard_dev-muuttujien on tarkoitus esittää logaritmia.

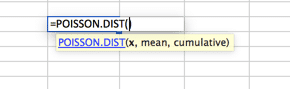
Poissonin jakauma

tämä on todennäköisesti kaikkein vajaakäytetyin jakauma. Oletuksena monet käyttävät normaalijakaumakäyrää, kun Poisson sopii malleilleen paremmin. Poisson on parhaiten kuvattu, kun on suuri jakauma lähellä aivan alussa, joka nopeasti hajoaa pitkä häntä toisella puolella. Esimerkki tästä olisi puhelinpalvelu, jossa puheluihin ei vastata ennen toista nollapistettä. Seurasi suurin osa puheluista vastasi ensimmäisen 2 välein (sanoa 30 ja 60 sekuntia) nopea pudotus volyymi ja pitkä häntä, hyvin harvat puhelut vastasi 20 minuuttia (väitetään).

tarkoituksena ei ole näyttää kaikkia mahdollisia jakaumia Excelissä, koska se ei kuulu tämän artikkelin soveltamisalaan. Pikemminkin varmistaa, että tiedät, että on olemassa monia vaihtoehtoja Monte Carlo simulointi. Älä lankea ansaan olettaen, että normaali jakelukäyrä sopii kaikkiin tietojen mallinnus. Jos haluat löytää lisää käyriä, siirry Excel-työkirjasi tilastollisiin toimintoihin ja tutki niitä. Jos sinulla on kysyttävää, esitä ne alla olevassa kommenttiosiossa.

rakentamalla mallin

tälle asetukselle oletetaan normaalijakauma ja 1 000 iteraatiota.

Input Variables

setup olettaa normaalijakauman. Normaalijakauma vaatii kolme muuttujaa; todennäköisyys, keskiarvo ja keskihajonta. Käsittelemme keskiarvoa ja keskihajontaa ensimmäisessä vaiheessa. Oletan rahoitusennuste ongelma, joka koostuu tuloista, muuttuvia ja kiinteitä kuluja. Jossa tulot miinus muuttuvat Kulut miinus kiinteät kulut on yhtä kuin voitto. Kiinteät kulut ovat uponneet laitoksiin ja laitteisiin, joten jakelukäyrää ei oleteta. Tulojen ja muuttuvien kulujen jakaumakäyrät oletetaan.

ensimmäinen simulaatio

alla olevassa esimerkissä esitetään tuloasetukset. Kaava voidaan kopioida ja liittää soluun D6 muuttuvia kuluja varten. Tulojen ja menojen Me sinulle toiminto normi.INV (), jossa parametrit ovat:

• todennäköisyys = funktio RAND (), jolla saadaan satunnaisluku jakauman muiden kriteerien perusteella.
• keskiarvo = vaiheessa 1 käytetty keskiarvo. Tulojen osalta se on C3.
• keskihajonta = vaiheessa 1 käytetty keskihajonta. Tulojen osalta se on C4

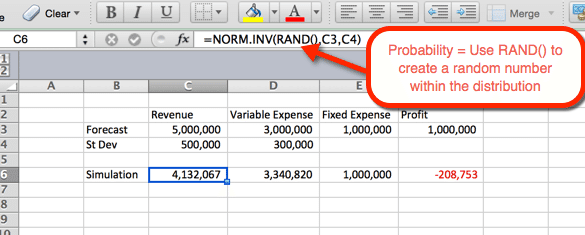
koska todennäköisyytenä käytetään randia (), syntyy satunnaistodennäköisyys päivityksessä. Käytämme tätä hyödyksemme seuraavassa vaiheessa.

1 000 simulaatiota

on olemassa useita tapoja tehdä 1 000 tai enemmän variaatiota. Yksinkertaisin vaihtoehto on ottaa kaava Vaihe #2 ja tehdä siitä absoluuttinen. Kopioi ja liitä 1000 kertaa. Yksinkertaista, mutta ei kovin hienoa. Ja jos Ferris Bueller voi pelastaa maailman näyttämällä uuden Tic Tac Toe-pelin tietokoneelle, voimme piristää tätäkin analyysiä. Mennään maailmaan pöytiä.

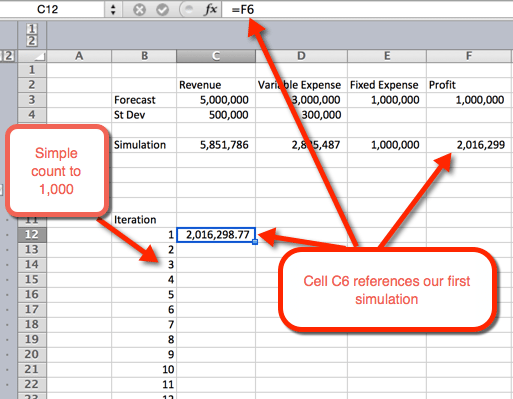
• ensin halutaan luoda hahmotelma taululle. Teemme tämän listaamalla numerot 1-1000 riveihin. Alla olevassa esimerkkikuvassa numerolista alkaa B12: sta.
• seuraavassa sarakkeessa, solussa C12, viitataan ensimmäiseen iteraatioon.

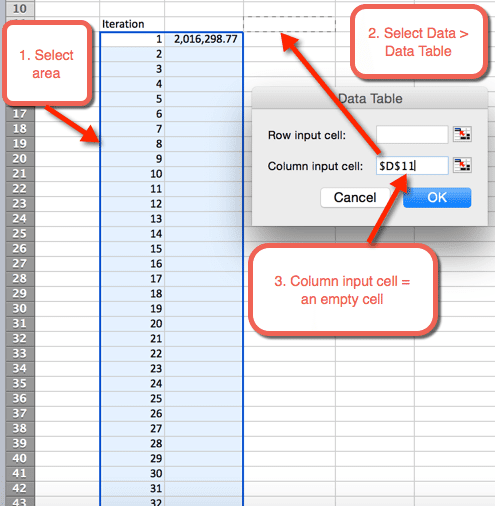
• korosta seuraavaksi alue, johon haluamme sijoittaa 1000 iteraatiota
• Valitse Data > datataulukot
• sarakkeen syöttökennolle: Valitse tyhjä solu. Ladattavassa tiedostossa solu D11 on valittu
• valitse OK

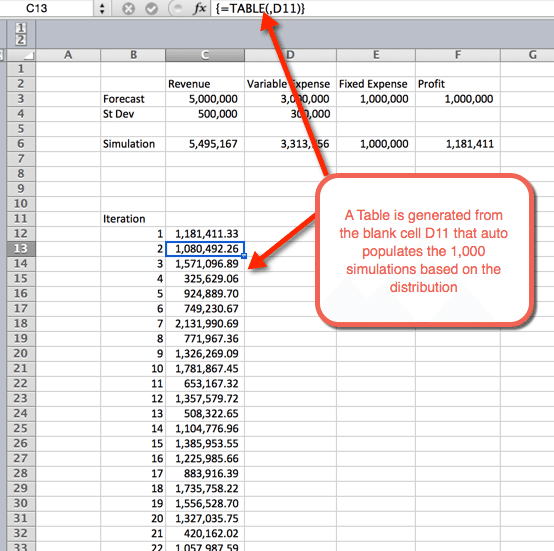
• kun OK on valittu edellisestä vaiheesta, lisätään taulukko, joka autopopuloi 1000 simulaatiot

yhteenvetotilastot

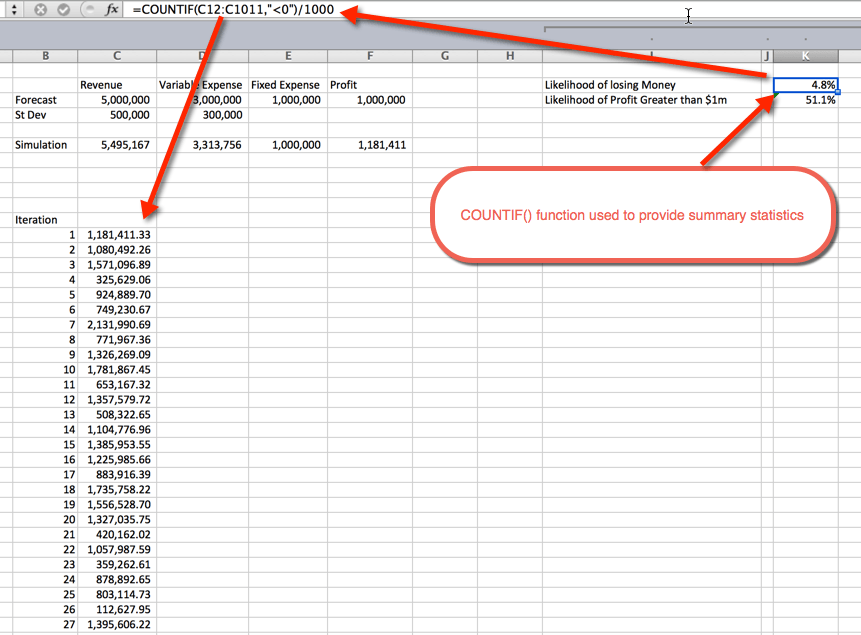
kun simulaatiot on suoritettu, on aika kerätä yhteenvetotilastot. Tämä voidaan tehdä useilla tavoilla. Tässä esimerkissä käytin COUNTIF () funktio määrittää prosenttiosuus simulaatioita, jotka ovat kannattamattomia, ja todennäköisyys voiton suurempi kuin $1 miljoonaa. Odotetusti, todennäköisyys suurempi kuin $1M leijuu noin 50%. Tämä johtuu siitä, että käytimme normaalijakauma käyrät, jotka ovat tasaisesti noin keskiarvo, joka oli $1m. todennäköisyys menettää rahaa on 4,8%. Tämä koottiin käyttämällä COUNTIF () – funktiota Nollaa pienempien simulaatioiden laskemiseen ja jakamalla 1 000 kokonaisseraatiolla.

Hanki lataus

yllä olevalla videolla oz kysyy Monte Carlon simulaation eri käyttötarkoituksista. Mihin olet käyttänyt sitä? Onko mitään erityisiä esimerkkejä, joita voit kertoa ryhmälle? Jos näin on, jätä huomautus alla kommentit osiossa. Myös, voit vapaasti rekisteröityä uutiskirjeemme, jotta voit pysyä ajan tasalla uutena Excel.TV keikat on julkistettu. Jätä minulle viesti alla pysyä yhteydessä.