sisältö (klikkaa siirtyäksesi kyseiseen osioon):

1. määritelmä & Formula_1264>
2. esimerkki
3. tulkintaongelmat
4. edut
5. kovarianssi Excelissä

määritelmä & Formula_9197>

kovarianssi on mitta siitä, kuinka paljon kaksi satunnaismuuttujaa vaihtelevat yhdessä. Se on samanlainen kuin varianssi, mutta jos varianssi kertoo, miten yksi muuttuja vaihtelee, co-varianssi kertoo, miten kaksi muuttujaa vaihtelevat yhdessä.

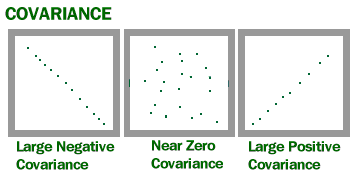
kuva U: sta Wisconsinista.

kovarianssin kaava

katso videolta esimerkki:

Etkö näe videota? Klikkaa tästä.

kaava on:
Cov (X, Y) = Σ E ((X-μ) E (Y-ν)) / n-1, jossa:

• X on satunnaismuuttuja
• e(X) = μ on satunnaismuuttujan X odotusarvo (keskiarvo) ja
• E(Y) = ν on satunnaismuuttujan Y
• n = tietoaineiston erien lukumäärä.
• Σ yhteenlaskettu merkintä.

takaisin alkuun

esimerkki

laske kovarianssi seuraavalle aineistolle:
x: 2.1, 2.5, 3.6, 4.0 (keskiarvo = 3.1)
y: 8, 10, 12, 14 (keskiarvo = 11)

korvaa arvot kaavaksi ja ratkaise:
cov(x,y) = σe((x-μ)(Y-ν)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267

tulos on positiivinen, eli muuttujat liittyvät positiivisesti toisiinsa.

Huomautus jaosta N: llä tai N-1:
kun käsitellään näytteitä, on olemassa N-1-termejä, joilla on vapaus vaihdella (katso: vapausasteet). Jos löydätte kahden satunnaismuuttujan kovarianssin, jakakaa SE n: llä.
takaisin alkuun

tulkintaongelmat

suuri kovarianssi voi tarkoittaa vahvaa suhdetta muuttujien välillä. Kuitenkin, et voi verrata variansseja yli tietojoukkojen eri asteikot (kuten kiloa ja tuumaa). Heikko kovarianssi yhdessä tietojoukossa voi olla vahva eri tietojoukossa, jossa on eri asteikot.

tulkinnan suurin ongelma on se, että sen ottamien tulosten laaja kirjo vaikeuttaa tulkintaa. Esimerkiksi tietokokonaisesi voi palauttaa arvon 3 tai 3000. Tämä laaja arvovalikoima johtuu yksinkertaisesta tosiasiasta; Mitä suuremmat X-ja Y-arvot, sitä suurempi on kovarianssi. Arvo 300 kertoo, että muuttujat korreloivat, mutta toisin kuin korrelaatiokerroin, tämä luku ei kerro tarkalleen, kuinka vahva kyseinen suhde on. Ongelma voidaan korjata jakamalla kovarianssi keskihajonnalla, jotta saadaan korrelaatiokerroin.
Corr (X, Y) = cov (X,Y) / σXσY
takaisin alkuun

korrelaatiokertoimen edut

Korrelaatiokertoimella on useita etuja kovarianssiin nähden suhteiden vahvuuksien määrittämisessä:

• kovarianssi voi kestää käytännössä minkä tahansa luvun, kun korrelaatio on rajoitettu: -1: stä + 1: een.
• sen numeeristen rajoitusten vuoksi korrelaatio on hyödyllisempää määriteltäessä, kuinka vahva suhde näiden kahden muuttujan välillä on.
• korrelaatiolla ei ole yksikköjä. Kovarianssilla on aina yksiköt
• korrelaatioon eivät vaikuta Keskuksen muutokset (ts. keskiarvo) tai muuttujien asteikko

takaisin alkuun

laske kovarianssi Excelissä

Katso video tai noudata alla olevia ohjeita (tämä on Excel 2013, mutta vaiheet ovat samat Excelissä 2016):

kovarianssi Excelissä: Overview

kovarianssi antaa positiivisen luvun, jos muuttujat liittyvät positiivisesti toisiinsa. Saat negatiivisen luvun, jos ne liittyvät negatiivisesti toisiinsa. Suuri kovarianssi viittaa periaatteessa siihen, että muuttujien välillä on vahva suhde. Alhainen arvo tarkoittaa heikkoa suhdetta.

kovarianssi Excelissä: vaiheet

Vaihe 1: syötä tietosi kahteen sarakkeeseen Excelissä. Kirjoita esimerkiksi X-arvosi sarakkeeseen A ja Y-arvosi sarakkeeseen B.

Vaihe 2: Napsauta ”Data” – välilehteä ja valitse sitten ”Data analysis.”Datan analysointi-ikkuna avautuu.

Vaihe 3: Valitse ”kovarianssi” ja valitse sitten ”OK.”

Vaihe 4: Napsauta ”Input Range” ja valitse sitten kaikki tietosi. Sisällytä sarakkeen otsikot, jos sinulla on niitä.

Vaihe 5: Napsauta ”Tarrat ensimmäisellä rivillä” – valintaruutua, jos olet sisällyttänyt sarakeotsikot tietovalintaasi.

Vaihe 6: Valitse ”Lähtöalue” ja valitse sitten alue laskentataulukosta. Hyvä paikka valita on alue, joka sijaitsee aivan tietosarjan oikealla puolella.

Vaihe 7: klikkaa ” OK.”Kovarianssi näkyy valitsemallasi alueella vaiheessa 5.

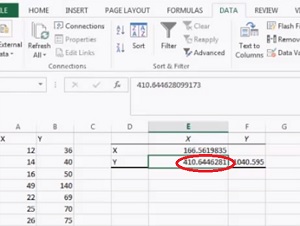
nyt riitti!

Vihje: Suorita korrelaatiofunktio Excelissä sen jälkeen, kun olet suorittanut kovarianssin Excelissä 2013. Korrelaatio antaa arvoa suhteelle. 1 on täydellinen korrelaatio ja 0 ei korrelaatiota. Kovarianssista näkee vain sen, onko suhteessa positiivista vai negatiivista.

Katso YouTube-kanavalta lisää Excel-vinkkejä ja ohjeita!

takaisin huipulle

Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). Sarjakuva opas tilastoja. HarperPerennial.

—————————————————————————

Tarvitsetko apua kotitehtävissä tai koekysymyksessä? Chegg Studyn avulla saat askelmittaisia ratkaisuja kysymyksiisi alan asiantuntijalta. Ensimmäinen 30 minuuttia Chegg tutor on ilmainen!