Hva Er Monte Carlo Simulering?

Monte Carlo Simulering er en Prosess med å bruke sannsynlighetskurver for å bestemme sannsynligheten for et utfall. Du kan klø deg i hodet her og si… «Hei Rick, en distribusjonskurve har en rekke verdier. Så hvordan bestemmer jeg sannsynligheten for et utfall?»Og enda bedre, hvordan gjør Jeg Det I Microsoft Excel uten noen spesiell add-insThought du aldri ville spørre.Dette gjøres ved å kjøre simuleringen tusenvis av ganger og analysere fordelingen av utgangen. Dette er spesielt viktig når du analyserer utgangen av flere distribusjonskurver som mates inn i hverandre.Eksempel:

• # Av Solgte Enheter kan ha en fordelingskurve
• multiplisert Med Markedspris, som kan ha en annen fordelingskurve
• minus variable lønninger som har en annen kurve
• etc., osv.

når alle disse fordelingene er blandet, kan utgangen være ganske kompleks. Kjører tusenvis av iterasjoner (eller simuleringer) av disse kurvene kan gi deg litt innsikt. Dette er spesielt nyttig for å analysere potensiell risiko for en beslutning.

Beskriv Monte Carlo

når jeg beskriver Monte Carlo-Simulering, refererer jeg ofte til 1980-tallets Film War Games, hvor en ung Mathew Broderick (før Ferris Bueller) er en hacker som bruker sitt oppringt modem for å hacke Seg Inn I Pentagon-datamaskinene og starte 3.Verdenskrig. Slags. Han fikk Pentagon-datamaskinene til å gjøre mange simuleringer Av spillene Tic Tac Toe for å lære datamaskinen at ingen vil en atomkrig-og redde verden i prosessen.Takk Ferris. Du er en helt.Her er et glimt av filmen for å vise deg big time Monte Carlo i aksjon. Jeg antar at du vil overse politikk, klosset mann klemmer og selvfølgelig, Dabney Coleman.

Distribusjonskurver

det finnes ulike distribusjonskurver du kan bruke til å sette Opp Monte Carlo-simuleringen. Og disse kurvene kan byttes ut basert på variabelen. Microsoft har ikke en formel kalt «Do Monte Carlo Simulation» i menylinjen:)

Uniform Distribution

i en jevn fordeling er det lik sannsynlighet hvor som helst mellom minimum og maksimum. En jevn fordeling ser ut som et rektangel.

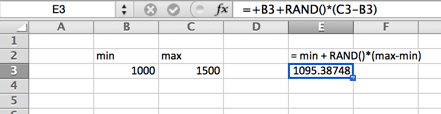
Normal (Gaussisk) Fordeling

Dette er også din standard klokkeformet kurve. Denne Monte Carlo Simuleringsformelen er preget av å være jevnt fordelt på hver side (median og gjennomsnitt er det samme – og ingen skjevhet). Haler av kurven går videre til uendelig. Så dette kan ikke være den ideelle kurven for boligpriser, hvor noen få topphus øker gjennomsnittet (gjennomsnittet) godt over medianen, eller i tilfeller der det er et hardt minimum eller maksimum. Et eksempel på dette kan være minstelønn i din locale. Vær oppmerksom på at navnet på funksjonen varierer avhengig av din versjon.

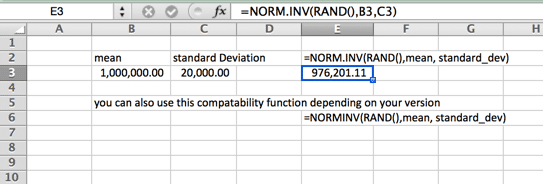
Lognormal Fordeling

en fordeling der logaritmen er normalfordelt med middel-og standardavviket. Så oppsettet ligner normalfordelingen, men vær oppmerksom på at middel-og standard_dev-variablene er ment å representere logaritmen.

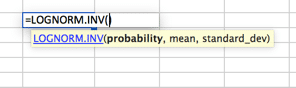
Poisson Distribusjon

Dette er sannsynligvis den mest underutnyttede fordelingen. Som standard bruker Mange mennesker en normalfordelingskurve når Poisson passer bedre til sine modeller. Poisson er best beskrevet når det er en stor fordeling nær begynnelsen som raskt sprer seg til en lang hale på den ene siden. Et eksempel på dette ville være et call center, der ingen samtaler besvares før andre NULL. Etterfulgt av flertallet av samtaler besvart i de første 2 intervaller (si 30 og 60 sekunder) med en rask nedgang i volum og en lang hale, med svært få samtaler besvart i 20 minutter (angivelig).

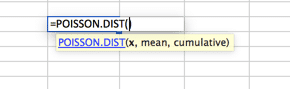
hensikten her er ikke å vise deg hver distribusjon som er mulig I Excel, da det er utenfor omfanget av denne artikkelen. Snarere for a sikre at du vet at det er mange alternativer tilgjengelig For Monte Carlo-Simuleringen din. Ikke fall i fellen for å anta at en normalfordelingskurve er riktig passform for all datamodellering. For å finne flere kurver, gå De Statistiske Funksjonene I Excel-arbeidsboken og undersøke. Hvis du har spørsmål, legg dem i kommentarfeltet nedenfor.

Bygge Modellen

for dette oppsettet vil vi anta en normalfordeling og 1000 iterasjoner.

Inndatavariabler

oppsettet forutsetter en normal fordeling. En normalfordeling krever tre variabler; sannsynlighet, gjennomsnitt og standardavvik. Vi vil takle gjennomsnittet og standardavviket i vårt første trinn. Jeg antar et finansprognoseproblem som består av Inntekter, Variable Og Faste Utgifter. Hvor Inntekter minus Variable Utgifter minus Faste Utgifter er Lik Fortjeneste. De Faste utgiftene er senket kostnad i anlegg og utstyr, så ingen distribusjonskurve antas. Distribusjonskurver antas For Inntekter og Variable Utgifter.

Første Simulering

eksemplet nedenfor angir Innstillingene for Inntekter. Formelen kan kopieres og limes inn i celle D6 for variable utgifter. For Inntekter og utgifter vi deg funksjonen NORMEN.INV () hvor parameterne er:

• Sannsynlighet = funksjonen RAND () for å fremkalle et tilfeldig tall basert på de andre kriteriene i fordelingen.
• Gjennomsnitt = gjennomsnittet brukt I Trinn 1. For Inntekter Er Det C3.
• Standardavvik = Standardavviket som brukes I Trinn 1. For Inntekter Er Det C4

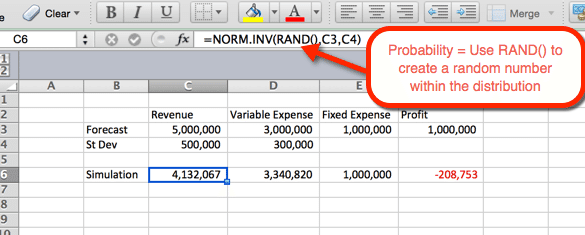
SIDEN RAND () brukes som sannsynlighet, genereres en tilfeldig sannsynlighet ved oppdatering. Vi vil bruke dette til vår fordel i neste trinn.

1000 Simuleringer

det er flere måter å gjøre 1000 eller flere variasjoner på. Det enkleste alternativet er å ta formelen fra trinn # 2 og gjøre det absolutt. Kopier og lim inn 1000 ganger. Det er enkelt, men ikke veldig fancy. Og Hvis Ferris Bueller kan redde verden ved å vise et Nytt Tic Tac Toe-spill til en datamaskin, så kan vi krydre denne analysen også. La oss våge inn i verden av tabeller.

• først vil vi lage en disposisjon for et bord. Vi gjør dette ved å liste tallene 1 til 1000 i rader. I eksempelbildet nedenfor starter nummerlisten I B12.
• i neste kolonne, i celle C12, vil vi referere til den første iterasjonen.

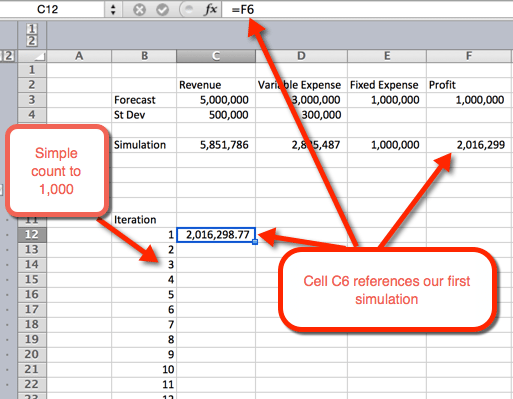
• neste markere området der vi ønsker å huse 1,000 iterasjoner
• Velg Data > Datatabeller
• For Kolonne input celle: Velg en tom celle. I nedlastingsfilen er celle D11 valgt
• Velg OK

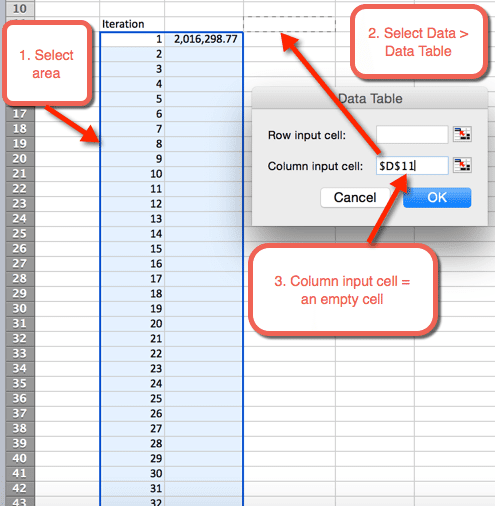
• NÅR OK er valgt fra forrige trinn, settes det inn et bord som autopopulerer de 1000 simuleringene

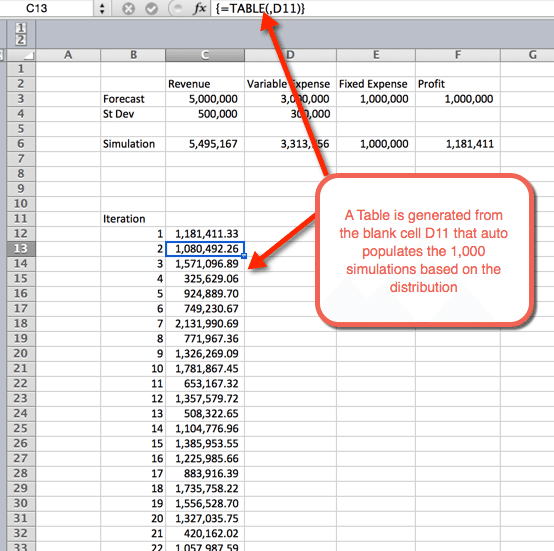
Sammendragsstatistikk

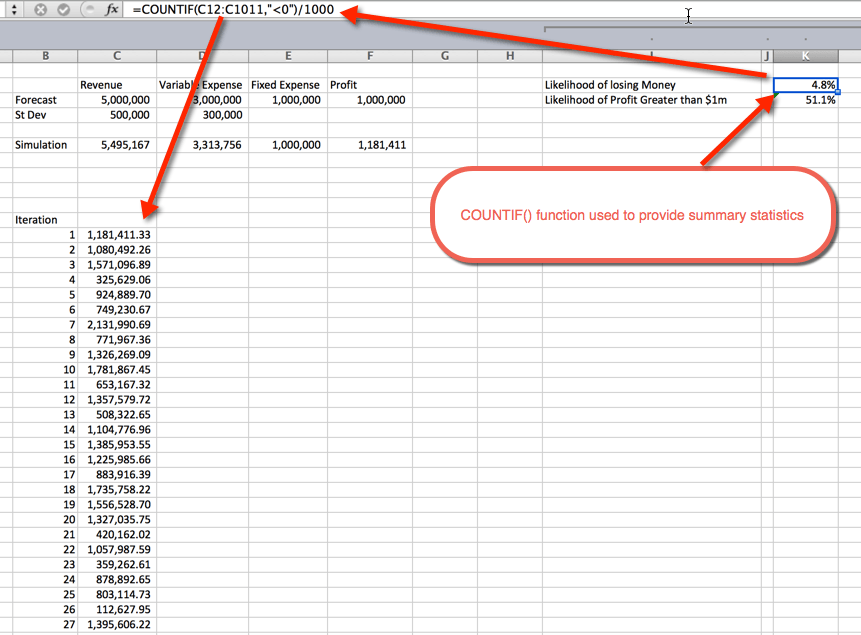
når simuleringene er kjørt, er det på tide å samle sammendragsstatistikk. Dette kan gjøres på flere måter. I dette eksemplet brukte JEG COUNTIF () – funksjonen for å bestemme prosentandelen av simuleringer som er ulønnsomme, og sannsynligheten for et overskudd større enn $1 Million. Som forventet svinger sannsynligheten for større enn $1m rundt 50%. Dette skyldes at vi brukte normalfordelingskurver som er jevnt fordelt rundt gjennomsnittet, som var $1m. sannsynligheten for å tape penger er 4,8%. DETTE ble samlet ved Å bruke COUNTIF () – funksjonen til å telle simuleringene som var mindre enn null, og dividere med de 1000 totale iterasjonene.

Få Nedlastingen

I videoen ovenfor spør Oz om De ulike bruksområdene For Monte Carlo-Simulering. Hva har du brukt den til? Er det noen konkrete eksempler som du kan dele med gruppen? Hvis ja, legg igjen et notat nedenfor i kommentarfeltet. Også, gjerne registrere deg for vårt nyhetsbrev, slik at du kan holde deg oppdatert som ny Excel.TV show er annonsert. Legg igjen en beskjed nedenfor for å holde kontakten.