Innholdsfortegnelse
- luftbrenselforhold definisjon
- luftbrenselforhold formel
- luftbrenselforhold for forskjellige drivstoff
- hvordan støkiometrisk luftbrenselforhold beregnes
- Lambda luftbrenselforhold
- Luftbrenselforhold og motorytelse
- Kalkulator For Luftbrenselforhold
- Påvirkning Av Luftbrenselforhold på motorutslipp
- lambda lukket forbrenningskontroll
definisjon av luftbrenselforhold
termiske motorer bruker drivstoff og oksygen (fra luft) til å produsere energi gjennom forbrenning. For å garantere forbrenningsprosessen må visse mengder drivstoff og luft leveres i forbrenningskammeret. En fullstendig forbrenning finner sted når alt drivstoff er brent, i eksosgassen vil det ikke være mengder ubrent drivstoff.
luftbrenselforhold er definert som forholdet mellom luft og drivstoff i en blanding forberedt for forbrenning. For eksempel, hvis vi har en blanding av metan og luft som har luftbrenselforholdet på 17,5, betyr det at i blandingen har vi 17,5 kg luft og 1 kg metan.
det ideelle (teoretiske) luftbrenselforholdet, for en fullstendig forbrenning, kalles støkiometrisk luftbrenselforhold. For en bensinmotor er det støkiometriske luftbrenselforholdet rundt 14,7: 1. Dette betyr at for å brenne helt 1 kg drivstoff trenger vi 14,7 kg luft. Forbrenningen er mulig selv OM AFR er forskjellig fra støkiometrisk. For at forbrenningsprosessen skal finne sted i en bensinmotor, er MINIMUM AFR rundt 6: 1 og maksimumet kan gå opp til 20:1.
når luftbrenselforholdet er høyere enn det støkiometriske forholdet, kalles luftbrenselblandingen mager. Når luftbrenselforholdet er lavere enn det støkiometriske forholdet, kalles luftbrenselblandingen rik. FOR eksempel, for en bensinmotor, ER EN AFR på 16,5: 1 mager og 13,7: 1 er rik.
Gå tilbake
formel for luftbrensel
i sammenheng med forbrenningsmotorer er luftbrenselforhold (AF eller AFR) definert som forholdet mellom massen av luft ma og masse drivstoff mf, som brukes av motoren når den kjører:
\{AFR = \frac{m_a}{m_f}} \tag{1}\]
det inverse forholdet kalles drivstoff-luftforhold (FA eller FAR) og det beregnes som:
\
Gå tilbake
luftbrenselforhold for forskjellige drivstoff
i tabellen nedenfor kan vi se det støkiometriske luftbrenselforholdet for flere fossile brensler.
| Drivstoff | Kjemisk formel | AFR |
| Metanol | CH3OH | 6.47:1 |
| Etanol | C2H5OH | 9:1 |
| Butanol | C4H9OH | 11,2:1 |
| Diesel | C12H23 | 14.5:1 |
| Bensin | C8H18 | 14.7:1 |
| Propan | C3H8 | 15.67:1 |
| Metan | CH4 | 17.19:1 |
| Hydrogen | H2 | 34.3:1 |
Kilde: wikipedia.org
for eksempel, for å brenne helt 1 kg etanol, trenger vi 9 kg luft og å brenne 1 kg diesel, vi trenger 14,5 kg luft.
Spark ignition (SI) motorer kjører vanligvis på bensin (bensin) drivstoff. AFR PÅ si-motorer varierer innenfor området 12: 1 (rik) til 20: 1 (mager), avhengig av motorens driftstilstand(temperatur, hastighet, last, etc.). Moderne forbrenningsmotorer opererer så mye som mulig rundt den støkiometriske AFR(hovedsakelig av gassetterbehandlingsgrunner). I tabellen nedenfor kan du se et eksempel PÅ EN SI-MOTOR AFR, funksjon av motorturtall og dreiemoment.
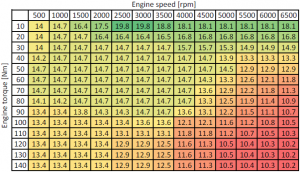
Bilde: EKSEMPEL på AIR fuel ratio (AFR) funksjon av motorturtall og dreiemoment
Compression ignition (CI) motorer vanligvis kjører på diesel. På grunn av forbrenningsprosessen kjører CI-motorer alltid på magre blandinger, MED AFR mellom 18: 1 og 70:1. Hovedforskjellen, sammenlignet MED si-motorer, er AT CI-motorer kjører på stratifiserte (ikke-homogene) luftbrenselblandinger, MENS SI kjører på homogene blandinger (ved portinjeksjonsmotorer).
tabellen ovenfor er skrevet Inn I Et scilab-skript og en konturplot genereres.
EngSpd_rpm_X = ;EngTq_Nm_Y = ;EngAFR_rat_Z = ;contour(EngSpd_rpm_X,EngTq_Nm_Y,EngAFR_rat_Z',30)xgrid()xlabel('Engine speed ')ylabel('Engine torque ')title('x-engineer.org')
Kjører scilab instruksjonene ovenfor vil generere følgende kontur plot:

Bilde: Air fuel contour plot Med Scilab
Gå tilbake
hvordan støkiometrisk luftbrenselforhold beregnes
for å forstå hvordan det støkiometriske luftbrenselforholdet beregnes, må vi se på forbrenningsprosessen av drivstoffet. Forbrenning er i utgangspunktet en kjemisk reaksjon (kalt oksidasjon) der et drivstoff blandes med oksygen og produserer karbondioksid (CO2), vann (H2O) og energi (varme). Ta hensyn til at for at oksidasjonsreaksjonen skal skje, trenger vi en aktiveringsenergi (gnist eller høy temperatur). Nettoreaksjonen er også svært eksoterm (med varmeutslipp).
\{gnist \tekst{ (SI)}} \tekst{Karbondioksid} + \tekst{Vann} + \tekst{Energi}\]
Eksempel 1. For en bedre forståelse, la oss se på oksidasjonsreaksjonen av metan. Dette er en ganske vanlig kjemisk reaksjon, siden metan er den primære komponenten av naturgass (i forhold til rundt 94 %).
Trinn 1. Skriv kjemisk reaksjon (oksidasjon)
\
Trinn 2. Balansere ligningen
\
Trinn 3. Skriv ned standard atomvekt for hvert atom
\
Trinn 4. Beregn massen av drivstoff, som er 1 mol metan, består av 1 atom karbon og 4 atomer av hydrogen.
\
Trinn 5. Beregn massen av oksygen, som består av 2 mol, hver mol består av 2 atomer oksygen.
\
Trinn 6. Beregn den nødvendige massen av luft som inneholder den beregnede massen av oksygen, med tanke på at luft inneholder rundt 21 % oksygen.
\
Trinn 7. Beregn luftbrenselforholdet ved hjelp av ligning (1)
\
DEN beregnede AFR for metan er ikke akkurat som spesifisert i litteraturen. Forskjellen kan komme fra det faktum at vi i vårt eksempel gjorde flere forutsetninger (luft inneholder bare 21% oksygen, forbrenningsproduktene er bare karbondioksid og vann).
Eksempel 2. Den samme metoden kan brukes for forbrenning av bensin. Med tanke på at bensin består av iso-oktan (C8H18), beregne støkiometrisk luftbrenselforhold for bensin.
Trinn 1. Skriv kjemisk reaksjon (oksidasjon)
\
Trinn 2. Balansere ligningen
\
Trinn 3. Skriv ned standard atomvekt for hvert atom
\
Trinn 4. Beregn massen av drivstoff, som er 1 mol iso-oktan, består av 8 atomer karbon og 18 atomer av hydrogen.
\
Trinn 5. Beregn massen av oksygen, som består av 12,5 mol, hver mol består av 2 atomer oksygen.
\
Trinn 6. Beregn den nødvendige massen av luft som inneholder den beregnede massen av oksygen, med tanke på at luft inneholder rundt 21 % oksygen.
\
Trinn 7. Beregn luftbrenselforholdet ved hjelp av ligning (1)
\
Igjen er det beregnede støkiometriske luftbrenselforholdet for bensin litt annerledes enn det som er gitt i litteraturen. Dermed er resultatet akseptabelt siden vi har gjort mange forutsetninger (bensin inneholder bare iso-oktan, luft inneholder bare oksygen i forhold til 21 %, de eneste forbrenningsproduktene er karbondioksid og vann, forbrenningen er ideell).
Gå tilbake
Lambda air fuel ratio
Vi har sett hva som er og hvordan du beregner det støkiometriske (ideelle) luftbrenselforholdet. I virkeligheten fungerer forbrenningsmotorer ikke akkurat med ideell AFR, men med verdier nær det. Derfor har VI et ideelt OG et faktisk LUFTBRENSEL AFR-forhold. Forholdet mellom det faktiske luftbrenselforholdet (AFRactual) og det ideelle/støkiometriske luftbrenselforholdet (AFRideal) kalles ekvivalens luftbrenselforhold eller lambda (λ).
\{\lambda = \frac{AFR_{actual}}{AFR_ {ideal}}} \ tag{3}\]
for eksempel er det ideelle luftbrennstoffforholdet for en bensinmotor 14,7:1. HVIS den faktiske/ekte AFR er 13,5, vil ekvivalensfaktoren lambda være:
\
avhengig av verdien av lambda, blir motoren fortalt å arbeide med magert, støkiometrisk eller rik luftbrenselblanding.
| Ekvivalens faktor | Luft drivstofforbruk blanding type | Beskrivelse |
| λ < 1.00 | Rik | Det er ikke nok luft til å brenne helt mengden drivstoff; etter forbrenning det er unburnt drivstoff i eksosgassen |
| λ = 1.00 | Stoichiometric (ideelt) | massen av luft er nøyaktig for en fullstendig forbrenning av drivstoff, og etter forbrenning, det er ingen ekstra oksygen i eksosen, og ingen unburnt drivstoff |
| λ > 1.00 | Lene | Det er mer oksygen enn nødvendig for å brenne helt mengden drivstoff; etter forbrenning er det overflødig oksygen i eksosgassene |
avhengig av type drivstoff (bensin eller diesel) og type injeksjon (direkte eller indirekte), kan en forbrenningsmotor fungere med magre, støkiometriske eller rike luftbrenselblandinger.

Bilde: Ecoboost 3-sylindret direkte injeksjon bensinmotor (lambda kart)
Kreditt: Ford
For eksempel Kjører Ford Ecoboost 3-sylindret motor med støkiometrisk luftbrenselforhold for tomgang til middels motorhastighet og komplett lastområde, og med rik luftbrenselblanding ved høy hastighet og belastning. Årsaken til hvilken den går med rik blanding ved høy motorturtall og belastning er motorkjøling. Det ekstra drivstoffet (som forblir ubrent) injiseres for å absorbere varme (gjennom fordampning), og reduserer dermed temperaturen i forbrenningskammeret.

Bilde: Dieselmotor (lambda kart)
Kreditt: wtz. de
en kompresjonstenningsmotor (diesel) kjører hele tiden med lean air drivstoffblanding, verdien av ekvivalensfaktoren (λ) avhengig av motorens driftspunkt (hastighet og dreiemoment). Årsaken til dette er arbeidsprinsippet til en dieselmotor: styring av last ikke gjennom luftmasse (som alltid er over), men gjennom drivstoffmasse (injeksjonstid).
Husk at en støkiometrisk ekvivalensfaktor (λ = 1,00) betyr et luftbrenselforhold på 14,7: 1 for bensinmotorer og 14,5: 1 for dieselmotorer.
Gå tilbake
luftbrenselforhold og motorytelse
motorens ytelse når det gjelder effekt og drivstofforbruk er svært avhengig av luftbrenselforholdet. For en bensinmotor oppnås det laveste drivstofforbruket ved magert AFR. Hovedårsaken er at det er nok oksygen tilgjengelig for å brenne helt alt drivstoffet som oversetter i mekanisk arbeid. På den annen side oppnås maksimal effekt med rike luftbrenselblandinger. Som forklart tidligere, legger mer drivstoff i sylinderen ved høy motorbelastning og hastighet, kjøler ned forbrenningskammeret (gjennom brennstofffordampning og varmeabsorpsjon) som gjør at motoren kan produsere maksimalt motormoment og dermed maksimal effekt.

Bilde: Motorkraft og drivstofforbruk funksjon av luftbrenselforhold (lambda)
i figuren ovenfor kan vi se at vi ikke kan få maksimal effekt på motoren og det laveste drivstofforbruket med samme luftbrenselforhold. Laveste drivstofforbruk (beste drivstofføkonomi) oppnås med blandinger av magre luftbrensler, MED EN AFR på 15,4: 1 og en ekvivalensfaktor (λ) på 1,05. Maksimal motorkraft produseres med rike luftbrenselblandinger, MED EN AFR på 12,6: 1 og en ekvivalensfaktor (λ) på 0,86. Med en støkiometrisk luftbrenselblanding (λ = 1) er det et kompromiss mellom maksimal motoreffekt og minimum drivstofforbruk.
Kompresjonstenningsmotorer (dieselmotorer) kjører alltid på blandinger av magert luftbrensel (λ > 1,00). De fleste moderne dieselmotorer kjører med λ mellom 1.65 og 1.10. Maksimal effektivitet (lavest drivstofforbruk) oppnås rundt λ = 1.65. Å øke drivstoffmengden over denne verdien (går mot 1,10) vil produsere mer sot (ubrente drivstoffpartikler).
det er en interessant studie utført Av R. Douglas på 2-takts syklusmotorer. I doktoravhandlingen «Closed Cycle Studies of A Two-Takts Cycle Engine» kommer R. Douglas med et matematisk uttrykk for ekvivalensfaktorens forbrenningseffektivitet (ηλ) (λ) funksjon.
for gnisttenning (bensinmotor) med en ekvivalensfaktor mellom 0,80 og 1.20, forbrenningseffektiviteten er:
\
for kompresjonstenning (dieselmotor)med en ekvivalensfaktor mellom 1,00 og 2,00, forbrenningseffektiviteten er:
\
for dieselmotorer, hvis ekvivalensfaktoren går over 2,00, er forbrenningseffektiviteten maksimal (1,00 eller 100%).
Vi kan bruke Et Scilab-skript for å plotte variasjonen av forbrenningseffektivitetsfunksjonen til ekvivalensfaktoren.
lmbd_g = ;lmbd_d = ;eff_lmbd_g = -1.6082+4.6509*lmbd_g-2.0746*lmbd_g.^2;eff_lmbd_d = -4.18+8.87*lmbd_d-5.14*lmbd_d.^2+lmbd_d.^3;plot(lmbd_g,eff_lmbd_g,'b','LineWidth',2)holdplot(lmbd_d,eff_lmbd_d,'r','LineWidth',2)xgrid()xlabel('$\lambda \text{ }$')ylabel('$\eta_{\lambda} \text{ }$')title('x-engineer.org')legend('gasoline','diesel',4)
Kjører scilab instruksjonene ovenfor utganger følgende grafiske vindu.

Bilde: Forbrenning effektivitet funksjon av ekvivalens faktor
som du kan se, komprimering tenning (diesel) motor, ved støkiometrisk luft drivstoff forholdet har en meget lav forbrenningseffektivitet. Den beste forbrenningseffektiviteten oppnås ved λ = 2.00 for diesel og λ = 1.12 for gnisttenningsmotorer (bensin).
Gå tilbake
kalkulator for luftbrensel
| ma | Drivstofftype Beregn |
λ |
| mf | ηλ |
Observasjon: forbrenningseffektiviteten beregnes bare for diesel og bensin (bensin) drivstoff, ved hjelp av ligningene (4) og (5). For de andre drivstoffene er forbrenningseffektivitetsberegningen ikke tilgjengelig (NA).
Gå tilbake
Påvirkning av luftbrenselforhold på motorutslipp
Forbrenningsmotorens avgassutslipp er avhengig av luftbrenselforholdet (ekvivalensfaktor). De viktigste avgassutslippene I ICE er oppsummert i tabellen nedenfor.
| Avgassutslipp | Beskrivelse |
| CO | karbonmonoksid |
| HC | hydrokarbon |
| NOx | nitrogenoksider |
| Sot | ubrente brenselpartikler |
FOR en bensinmotor er CO, HC og NOx avgassutslipp sterkt påvirket av luftbrenselforhold. CO og HC produseres hovedsakelig med rik luftbrenselblanding, Mens NOx med magre blandinger. Så, det er ingen fast luftbrenselblanding som vi kan få minimum for alle eksosutslipp.

Bilde: Bensinmotor katalysator effektivitet funksjon av luft drivstoff ratio
en treveis katalysator (TWC), som brukes for bensinmotorer, har den høyeste effektivitet når motoren opererer i et smalt bånd rundt støkiometrisk luft drivstoff ratio. TWC konverterer mellom 50 … 90% hydrokarboner og 90 … 99% karbonmonoksid og nitrogenoksider, når motoren går med λ = 1.00.
Gå tilbake
Lambda lukket forbrenningskontroll
for å oppfylle avgassutslippsforskriftene er det avgjørende for forbrenningsmotorer (spesielt bensin) å ha en nøyaktig kontroll over luftbrenselforholdet. Derfor har alle moderne forbrenningsmotorer lukket styring for luftbrenselforhold (lambda).

Bilde: Forbrenningsmotor lukket sløyfe lambda kontroll (bensinmotorer)
- luftmassestrømsensor
- primær katalysator
- sekundær katalysator
- drivstoffinnsprøytning
- oppstrøms lambda (oksygen) sensor
- nedstrøms lambda (oksygen) sensor
- drivstofftilførselskrets
- inntaksmanifold
- eksosmanifold
den kritiske komponenten for at systemet skal fungere er lambda (oksygen) sensoren. Denne sensoren måler nivået av oksygenmolekyler i eksosgassen og sender informasjonen til motorens elektroniske styreenhet (ECU). Basert på verdien av oksygensensoravlesningen vil BENSINMOTORENS ECU justere nivået av drivstoffmasse for å holde luftbrenselforholdet rundt støkiometrisk nivå (λ = 1,00).
for eksempel (bensinmotorer), hvis nivået av oksygenmolekyler er over terskelen for støkiometrisk nivå (derfor har vi en mager blanding), ved neste injeksjonssyklus, vil den injiserte drivstoffmengden økes for å gjøre bruk av overflødig luft. Husk at motoren alltid vil overgang fra magert blanding til rik blanding mellom injeksjonssykluser, noe som vil gi et «gjennomsnitt» av støkiometriske luftbrenselblandinger/ – forhold.
for dieselmotorer, siden det alltid går på lean air drivstoffforhold, utføres lambda-kontrollen på en annen måte. Det endelige målet er fortsatt det samme, kontroll av eksosgassutslippene.