Contenuti (fare Clic per passare alla sezione):

1. Definizione & Formula
2. Esempio
3. Problemi con l’Interpretazione
4. Vantaggi
5. Covarianza in Excel

Definizione & Formula

Covarianza è una misura di quanto due variabili casuali variare insieme. È simile alla varianza, ma dove la varianza ti dice come varia una singola variabile, la varianza co ti dice come due variabili variano insieme.

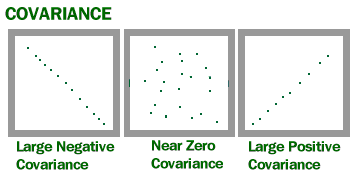
Immagine da U del Wisconsin.

La formula di covarianza

Guarda il video per un esempio:

Non riesci a vedere il video? Clicca qui.

La formula è:
Cov (X, Y) = Σ E ((X – μ) E (Y – ν)) / n-1 dove:

• X è una variabile casuale
• E(X) = µ è il valore atteso (media) della variabile casuale X e
• E(Y) = ν è il valore atteso (media) della variabile casuale Y
• n = numero di elementi nel set di dati.
• Σ notazione di somma.

Torna all’inizio

Esempio

Calcolare la covarianza per la seguente serie di dati:
x: 2.1, 2.5, 3.6, 4.0 (media = 3.1)
y: 8, 10, 12, 14 (media = 11)

Sostituire i valori nella formula e risolvere:
Cov(X,Y) = ΣE((X-µ)(Y-n)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267

Il risultato è positivo, il che significa che le variabili sono correlate positivamente.

Nota sulla divisione per n o n-1:
Quando si tratta di campioni, ci sono termini n-1 che hanno la libertà di variare (vedi: Gradi di libertà). Se stai trovando la covarianza di solo due variabili casuali, dividi per n.
Torna all’inizio

Problemi di interpretazione

Una covarianza ampia può significare una forte relazione tra variabili. Tuttavia, non è possibile confrontare le varianze su set di dati con scale diverse (come libbre e pollici). Una covarianza debole in un set di dati può essere forte in un set di dati diverso con scale diverse.

Il problema principale dell’interpretazione è che l’ampia gamma di risultati che assume rende difficile l’interpretazione. Ad esempio, il set di dati potrebbe restituire un valore di 3 o 3.000. Questa vasta gamma di valori è causata da un semplice fatto; Più grandi sono i valori X e Y, maggiore è la covarianza. Un valore di 300 ci dice che le variabili sono correlate, ma a differenza del coefficiente di correlazione, quel numero non ci dice esattamente quanto sia forte quella relazione. Il problema può essere risolto dividendo la covarianza per la deviazione standard per ottenere il coefficiente di correlazione.
Corr (X,Y) = Cov (X,Y) / σXσY
Torna su

Vantaggi del coefficiente di correlazione

Il coefficiente di correlazione presenta diversi vantaggi rispetto alla covarianza per determinare i punti di forza delle relazioni:

• La covarianza può assumere praticamente qualsiasi numero mentre una correlazione è limitata: da -1 a +1.
• A causa delle sue limitazioni numeriche, la correlazione è più utile per determinare quanto sia forte la relazione tra le due variabili.
• La correlazione non ha unità. La covarianza ha sempre unità
• La correlazione non è influenzata dai cambiamenti nel centro (cioè la media) o la scala delle variabili

Torna all’inizio

Calcolare la Covarianza in Excel

Guarda il video o seguire la procedura descritta di seguito (questo è per Excel 2013, ma i passaggi sono gli stessi per Excel 2016):

Covarianza in Excel: Panoramica

Covarianza ti dà un numero positivo se le variabili sono positivamente correlati. Otterrai un numero negativo se sono correlati negativamente. Un’alta covarianza indica fondamentalmente che esiste una forte relazione tra le variabili. Un valore basso significa che c’è una relazione debole.

Covarianza in Excel: Passi

Passo 1: Inserisci i tuoi dati in due colonne in Excel. Ad esempio, digitare i valori X nella colonna A e i valori Y nella colonna B.

Passo 2: Fare clic sulla scheda “Dati” e quindi fare clic su “Analisi dei dati.”Si aprirà la finestra di analisi dei dati.

Passo 3: Scegliere “Covarianza” e quindi fare clic su ” OK.”

Passo 4: Fare clic su “Intervallo di input” e quindi selezionare tutti i dati. Includi le intestazioni delle colonne se le hai.

Passaggio 5: Fare clic sulla casella di controllo” Etichette in prima riga ” se sono state incluse le intestazioni di colonna nella selezione dei dati.

Passo 6: selezionare “Intervallo di output” e quindi selezionare un’area sul foglio di lavoro. Un buon posto per selezionare è un’area appena a destra del set di dati.

Passo 7: Fare clic su “OK.”La covarianza apparirà nell’area selezionata nel passaggio 5.

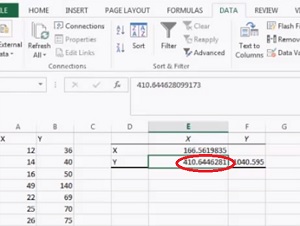
Ecco fatto!

Suggerimento: eseguire la funzione di correlazione in Excel dopo aver eseguito la covarianza in Excel 2013. Correlazione vi darà un valore per la relazione. 1 è correlazione perfetta e 0 non è correlazione. Tutto quello che puoi davvero dire dalla covarianza è se c’è una relazione positiva o negativa.

Controlla il nostro canale YouTube per ulteriori suggerimenti di Excel e aiuto!

Torna su

Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). La Guida fumetto per le statistiche. HarperPerennial.

—————————————————————————

Hai bisogno di aiuto con un compito a casa o una domanda di prova? Con Chegg Studio, è possibile ottenere soluzioni passo-passo alle vostre domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!