mi az a Monte Carlo szimuláció?

a Monte Carlo szimuláció a valószínűségi görbék használatának folyamata az eredmény valószínűségének meghatározására. Itt megvakarhatja a fejét, és elmondhatja… “Hé Rick, az eloszlási görbének számos értéke van. Tehát hogyan határozhatom meg pontosan az eredmény valószínűségét?”És még jobb, Hogyan tudom ezt megtenni a Microsoft Excelben anélkül, hogy bármilyen speciális kiegészítőt használnék, gondoltam, hogy soha nem kérdeznéd meg.Ez a szimuláció több ezer alkalommal történő futtatásával és a kimenet eloszlásának elemzésével történik. Ez különösen akkor fontos, ha több elosztási görbe kimenetét elemzi, amelyek egymásba táplálkoznak.Példa:

• # az eladott egységek eloszlási görbéje
• szorozva a piaci árral, amelynek lehet egy másik eloszlási görbéje
• mínusz változó bérek, amelyeknek egy másik görbéje
• stb. stb.

miután ezek az eloszlások összekeveredtek, a kimenet meglehetősen összetett lehet. E görbe több ezer iterációjának (vagy szimulációjának) futtatása betekintést nyújthat. Ez különösen hasznos a döntés potenciális kockázatának elemzésében.

Description Monte Carlo

a Monte Carlo szimuláció leírásakor gyakran utalok az 1980-as évek háborús játékaira, ahol egy fiatal Mathew Broderick (Ferris Bueller előtt) egy hacker, aki telefonos modemjével feltöri a Pentagon számítógépeit, és elindítja a 3.világháborút. Olyasmi. Ezután a Pentagon számítógépeivel sok szimulációt készített a Tic Tac Toe játékokról, hogy megtanítsa a számítógépet arra, hogy senki sem fog nukleáris háborút indítani – és közben megmentse a világot.Köszönöm Ferris. Hős vagy.Itt egy pillantás a filmre, amely megmutatja a nagy idő Monte Carlo akcióban. Feltételezem, hogy figyelmen kívül hagyja a politikát, a kínos ember ölelését és természetesen Dabney Colemant.

eloszlási görbék

különböző eloszlási görbék használhatók a Monte Carlo szimuláció beállításához. Ezek a görbék a változó alapján felcserélhetők. A Microsoft nem rendelkezik a “Do Monte Carlo Simulation” nevű képlettel a menüsorban 🙂

egyenletes eloszlás

egyenletes eloszlásban a minimum és a maximum között bárhol azonos a valószínűsége. Az egyenletes eloszlás úgy néz ki, mint egy téglalap.

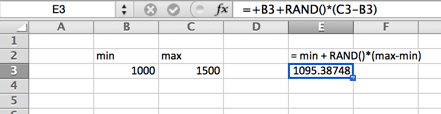
normál (Gauss-féle) Eloszlás

ez a szokásos harang alakú görbe is. Ezt a Monte Carlo szimulációs képletet az jellemzi, hogy egyenletesen oszlik el mindkét oldalon(a medián és az átlag ugyanaz – és nincs ferdeség). A görbe farka a végtelenbe megy. Tehát ez nem lehet az ideális görbe a lakásárakhoz, ahol néhány felső ház növeli az átlagot (átlag) jóval a medián felett, vagy olyan esetekben, amikor kemény minimum vagy maximum van. Erre példa lehet a helyi minimálbér. Felhívjuk figyelmét, hogy a funkció neve a verziótól függően változik.

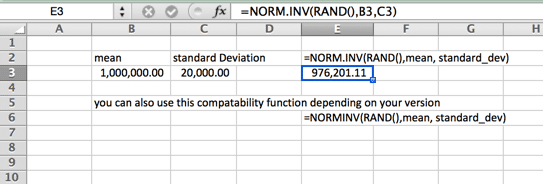
lognormális eloszlás

olyan Eloszlás, ahol a logaritmus normál eloszlású az átlaggal és a szórással. Tehát a beállítás hasonló a normál eloszláshoz, de kérjük, vegye figyelembe, hogy a mean és a standard_dev változók a logaritmust képviselik.

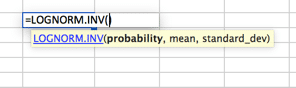
Poisson-eloszlás

ez valószínűleg a leginkább kihasználatlan Eloszlás. Alapértelmezés szerint sokan normál eloszlási görbét használnak, amikor a Poisson jobban megfelel a modelljeiknek. A Poisson-t akkor lehet a legjobban leírni, ha a legelején nagy Eloszlás van, amely az egyik oldalon gyorsan eloszlik egy hosszú farokig. Erre példa lehet egy call center, ahol a második nulla előtt nem fogadnak hívásokat. Ezt követi a hívások többsége az első 2 intervallumban (mondjuk 30 és 60 másodperc), gyors hangerő-csökkenéssel és hosszú farokkal, nagyon kevés hívással 20 perc alatt (állítólag).

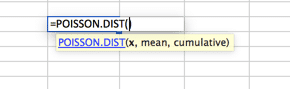
itt nem az a cél, hogy minden lehetséges terjesztést megjelenítsen az Excelben, mivel ez kívül esik a cikk hatályán. Inkább annak érdekében, hogy tudja, hogy sok lehetőség áll rendelkezésre a Monte Carlo szimuláció. Ne essen abba a csapdába, hogy feltételezzük, hogy a normál eloszlási görbe megfelelő az összes adatmodellezéshez. További görbék kereséséhez keresse meg az Excel munkafüzet statisztikai függvényeit, és vizsgálja meg. Ha kérdése van, tegye fel őket az alábbi megjegyzések részben.

a modell felépítése

ehhez a beállításhoz normál eloszlást és 1000 iterációt fogunk feltételezni.

bemeneti változók

a Beállítás normális eloszlást feltételez. A normális eloszláshoz három változó szükséges: valószínűség, átlag és szórás. Az első lépésben az átlagot és a szórást fogjuk kezelni. Feltételezem, hogy a pénzügyi előrejelzési probléma bevételekből, változó és fix kiadásokból áll. Ahol bevétel mínusz változó költségek mínusz fix költségek egyenlő nyereség. A fix költségek a gépek és berendezések süllyesztett költségei, tehát nem feltételezzük az elosztási görbét. Az elosztási görbéket a bevételek és a változó kiadások esetében feltételezzük.

első szimuláció

az alábbi példa a bevétel beállításait mutatja. A képlet másolható és beilleszthető a D6 cellába változó költségek esetén. A bevételek és kiadások mi a funkció norma.INV() ahol a paraméterek:

• valószínűség = a függvény RAND () véletlenszerű szám kiváltására az eloszláson belüli többi kritérium alapján.
• átlag = az 1.lépésben használt átlag. A bevétel szempontjából ez a C3.
• szórás = az 1.lépésben használt szórás. A bevétel szempontjából ez C4

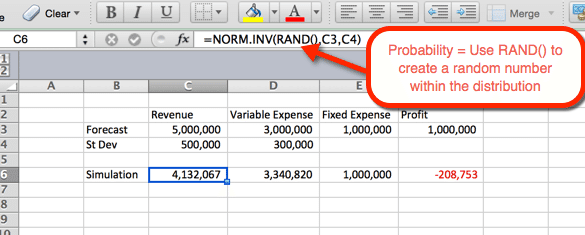
mivel a RAND () valószínűségként használatos, A frissítéskor véletlenszerű valószínűség keletkezik. Ezt a következő lépésben előnyünkre fogjuk használni.

1000 szimuláció

1000 vagy több variáció többféle módon is elvégezhető. A legegyszerűbb megoldás az, ha a képletet a 2. lépésből vesszük, és abszolútvá tesszük. Ezután másolja be 1000-szer. Ez egyszerű, de nem túl divatos. És ha Ferris Bueller meg tudja menteni a világot egy új Tic Tac Toe játék bemutatásával a számítógépre, akkor ezt az elemzést is feldobhatjuk. Menjünk be az asztalok világába.

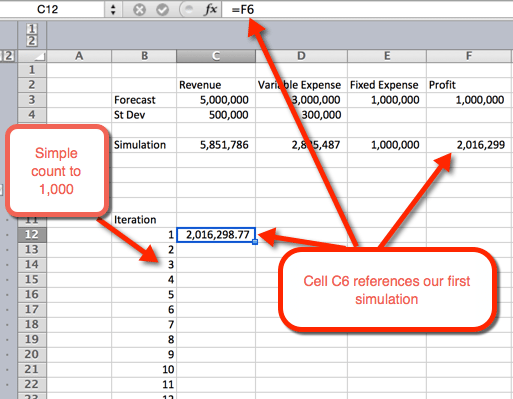
• először egy táblázat vázlatát szeretnénk létrehozni. Ezt úgy tesszük, hogy sorokban felsoroljuk az 1-1000 számot. Az alábbi példaképen a számlista B12-ben kezdődik.
• a következő oszlopban, a C12 cellában hivatkozunk az első iterációra.

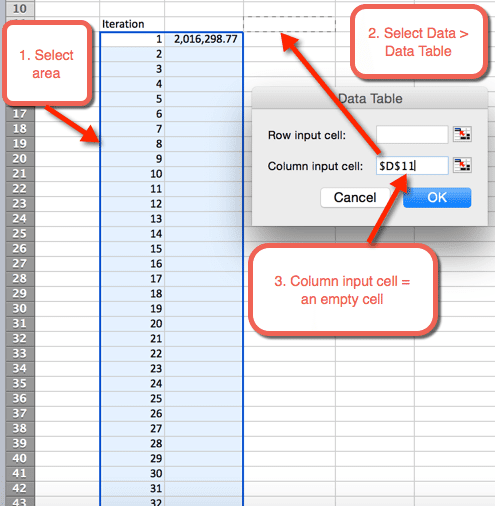
• ezután jelölje ki azt a területet, ahol az 1000 iterációt szeretnénk elhelyezni
• válassza ki az adatokat > adattáblák
• Oszlopbeviteli cellához: válasszon ki egy üres cellát. A letöltési fájlban a D11 cella van kiválasztva
• válassza az OK lehetőséget

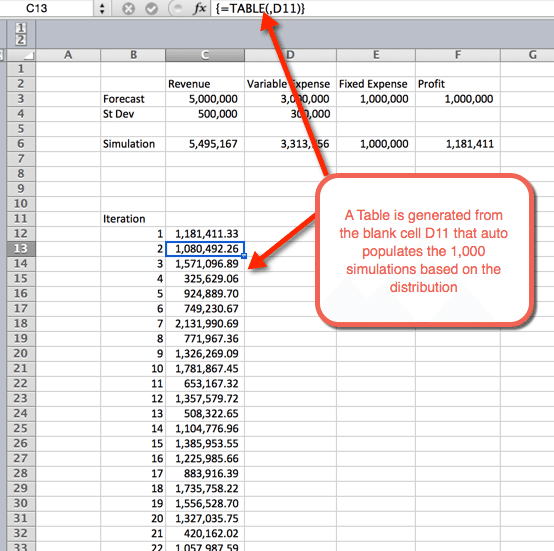
• Miután kiválasztotta az OK-t az előző lépésből, egy táblázat kerül beillesztésre, amely autopopulálja az 1000 szimulációt

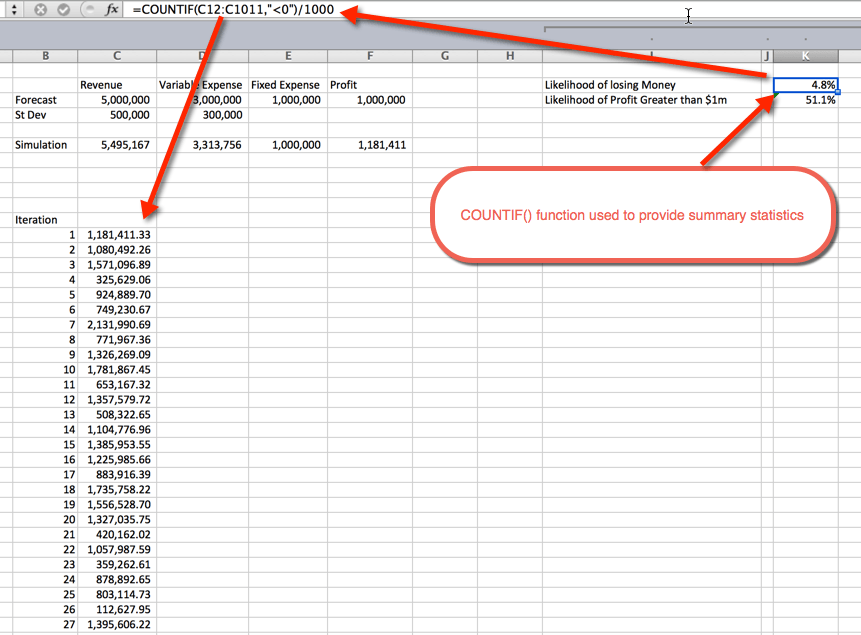
összefoglaló statisztikák

a szimulációk futtatása után ideje összefoglaló statisztikákat gyűjteni. Ezt meg lehet tenni számos módon. Ebben a példában a COUNTIF () függvényt használtam a veszteséges szimulációk százalékos arányának, valamint az 1 millió dollárnál nagyobb nyereség valószínűségének meghatározására. Ahogy az várható volt, az 1 millió dollárnál nagyobb valószínűség 50% körül mozog. Ennek oka az, hogy normál eloszlási görbéket használtunk, amelyek egyenletesen oszlanak el az átlag körül, ami 1 millió dollár volt. a pénzvesztés valószínűsége 4,8%. Ezt úgy gyűjtöttük össze, hogy a COUNTIF() függvény segítségével megszámoltuk a nullánál kisebb szimulációkat, és elosztottuk az 1000 teljes iterációval.

töltse le

a fenti videóban Oz a Monte Carlo szimuláció különféle felhasználásairól kérdez. Mire használtad? Vannak konkrét példák, amelyeket megoszthat a csoporttal? Ha igen, hagyjon egy megjegyzést alább a megjegyzések részben. Is, nyugodtan iratkozzon fel hírlevelünkre, hogy naprakész lehessen, mint új Excel.TV a műsorokat bejelentették. Hagyjon nekem egy üzenetet az alábbiakban, hogy kapcsolatban maradjak.