tartalom (kattintson az adott szakaszra való ugráshoz):

1. definíció & Formula
2. példa
3. értelmezési problémák
4. előnyök
5. kovariancia az Excelben

definíció & Formula

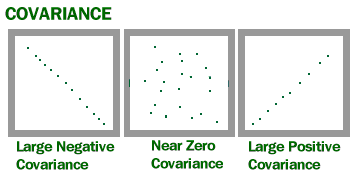
kovariancia annak mértéke, hogy mennyi két véletlen változó változik együtt. Hasonló a varianciához, de ahol a variancia megmondja, hogyan változik egyetlen változó, a co variancia megmutatja, hogyan változik két változó együtt.

kép a Wisconsini U-ból.

a kovariancia képlet

nézze meg a videót egy példa:

nem látja a videót? Kattints ide.

a képlet a következő:
Cov (X,Y) = 6 fő E ((X-fő) E (Y-fő)) / n-1, ahol:

• X egy véletlen változó
• E(X) = a véletlen változó várható értéke (átlaga) X és
• E(Y) = a véletlen változó várható értéke (átlaga) y
• n = az adathalmaz elemeinek száma.
• ons Összegzés.

vissza az elejére

példa

számítsa ki A kovarianciát a következő adatkészlethez:
x: 2.1, 2.5, 3.6, 4.0 (átlag = 3.1)
y: 8, 10, 12, 14 (átlag = 11)

cserélje ki az értékeket a képletbe,és oldja meg:
cov(x, y) = Ca-n((x-o-n)(y-o-n)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267

az eredmény pozitív, ami azt jelenti, hogy a változók pozitívan kapcsolódnak egymáshoz.

Megjegyzés Az N-vel vagy n-1-vel való elosztáshoz:
a minták kezelésekor vannak olyan n-1 kifejezések, amelyek szabadon változhatnak (lásd: szabadságfokok). Ha csak két véletlen változó kovarianciáját találja meg, csak ossza el n-vel.
vissza az elejére

értelmezési problémák

a nagy kovariancia erős kapcsolatot jelenthet a változók között. Nem lehet azonban összehasonlítani a különböző skálákkal (például fontokkal és hüvelykekkel) rendelkező adatkészletek eltéréseit. Egy gyenge kovariancia egy adathalmazban erős lehet egy másik adathalmazban, különböző skálákkal.

az értelmezés fő problémája az, hogy az eredmények széles skálája megnehezíti az értelmezést. Az adathalmaz például 3 vagy 3000 értéket adhat vissza. Ezt a széles értéktartományt egy egyszerű tény okozza; Minél nagyobb az X és Y érték, annál nagyobb a kovariancia. A 300-as érték azt jelzi, hogy a változók korrelálnak, de a korrelációs együtthatóval ellentétben ez a szám nem mondja meg pontosan, mennyire erős ez a kapcsolat. A probléma megoldható úgy, hogy A kovarianciát elosztjuk a szórással, hogy megkapjuk a korrelációs együtthatót.
Corr (X, Y) = Cov (X,Y) / adapt (x, y)
vissza az elejére

a korrelációs együttható előnyei

a korrelációs együtthatónak számos előnye van a kovarianciával szemben a kapcsolatok erősségének meghatározásában:

• a kovariancia gyakorlatilag bármilyen számot felvehet, míg a korreláció korlátozott: -1-től +1-ig.
• numerikus korlátai miatt a korreláció hasznosabb annak meghatározásához, hogy a két változó közötti kapcsolat milyen erős.
• a korrelációnak nincs egysége. A kovarianciának mindig vannak egységei
• a korrelációt nem befolyásolják a központ változásai (pl.

vissza az elejére

Számítsa ki A kovarianciát az Excelben

nézze meg a videót, vagy kövesse az alábbi lépéseket(ez az Excel 2013 esetében, de a lépések megegyeznek az Excel esetében 2016):

kovariancia az Excelben: áttekintés

a kovariancia pozitív számot ad, ha a változók pozitívan kapcsolódnak egymáshoz. Negatív számot kap, ha negatívan kapcsolódnak egymáshoz. A magas kovariancia alapvetően azt jelzi, hogy erős kapcsolat van a változók között. Az alacsony érték azt jelenti, hogy gyenge kapcsolat van.

kovariancia az Excelben: lépések

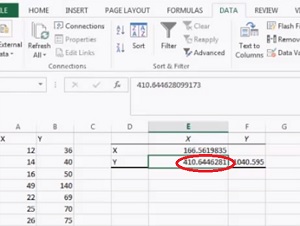
1. lépés: Írja be adatait két oszlopba az Excelben.

2. lépés: Kattintson az” adatok “fülre, majd az “adatelemzés” gombra.”Megnyílik az adatelemzés ablak.

3. lépés: Válassza a “kovariancia” lehetőséget, majd kattintson az “OK” gombra.”

4. lépés: Kattintson a “bemeneti tartomány” elemre, majd válassza ki az összes adatot. Tartalmazza az oszlopfejléceket, ha vannak ilyenek.

5. lépés: Kattintson a” címkék az első sorban ” jelölőnégyzetre, ha oszlopfejléceket tartalmazott az adatválasztásban.

6. lépés: Válassza a “kimeneti tartomány” lehetőséget, majd válasszon ki egy területet a munkalapon. Egy jó hely, hogy válasszon egy terület csak a jogot az adathalmaz.

7.lépés: Kattintson az “OK” gombra.”A kovariancia az 5. lépésben kiválasztott területen jelenik meg.

ez az!

tipp: futtassa a korrelációs függvényt az Excelben, miután futtatta A kovarianciát az Excel 2013 – ban. A korreláció értéket ad a kapcsolatnak. Az 1 tökéletes korreláció, a 0 pedig nincs korreláció. A kovarianciából csak annyit lehet megmondani, hogy van-e pozitív vagy negatív kapcsolat.

nézze meg YouTube csatornánkat további Excel tippekért és segítségért!

vissza a lap tetejére

Dodge, Y. (2008). A statisztikák Tömör enciklopédiája. Springer.
Everitt, B. S.; Skrondal, A. (2010), A Cambridge-i statisztikai szótár, Cambridge University Press.
Gonick, L. (1993). A rajzfilm útmutató a statisztikákhoz. HarperPerennial.

—————————————————————————

segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!