Qu’est-ce que la simulation Monte Carlo ?

La simulation de Monte Carlo est un processus qui consiste à utiliser des courbes de probabilité pour déterminer la probabilité d’un résultat. Vous pouvez vous gratter la tête ici et dire… « Hey Rick, une courbe de distribution a un tableau de valeurs. Alors, comment déterminer exactement la probabilité d’un résultat? »Et mieux encore, comment faire cela dans Microsoft Excel sans compléments spéciauxpensé que vous ne demanderiez jamais.Cela se fait en exécutant la simulation des milliers de fois et en analysant la distribution de la sortie. Ceci est particulièrement important lorsque vous analysez la sortie de plusieurs courbes de distribution qui s’alimentent les unes dans les autres.Exemple :

• Le nombre d’unités vendues peut avoir une courbe de distribution
• multipliée par le prix du marché, qui peut avoir une autre courbe de distribution
• moins les salaires variables qui ont une autre courbe
• etc., etc.

Une fois que toutes ces distributions sont entremêlées, la sortie peut être assez complexe. L’exécution de milliers d’itérations (ou de simulations) de ces courbes peut vous donner quelques informations. Ceci est particulièrement utile pour analyser le risque potentiel d’une décision.

Décrire Monte Carlo

En décrivant la Simulation de Monte Carlo, je me réfère souvent aux Jeux de guerre du cinéma des années 1980, où un jeune Mathew Broderick (avant Ferris Bueller) est un pirate informatique qui utilise son modem commuté pour pirater les ordinateurs du Pentagone et déclencher la 3e Guerre mondiale. En quelque sorte. Il a ensuite demandé aux ordinateurs du Pentagone de faire de nombreuses simulations des jeux Tic Tac Toe pour apprendre à l’ordinateur que personne ne fera une guerre nucléaire – et sauver le monde dans le processus.Merci Ferris. Tu es un héros.Voici un aperçu du film pour vous montrer le grand Monte Carlo en action. Je suppose que vous négligerez la politique, l’homme maladroit qui s’étreint et bien sûr, Dabney Coleman.

Courbes de distribution

Il existe différentes courbes de distribution que vous pouvez utiliser pour configurer votre simulation Monte Carlo. Et ces courbes peuvent être interchangées en fonction de la variable. Microsoft n’a pas de formule appelée « Faire une simulation de Monte Carlo » dans la barre de menu:)

Distribution uniforme

Dans une distribution uniforme, il y a une probabilité égale entre le minimum et le maximum. Une distribution uniforme ressemble à un rectangle.

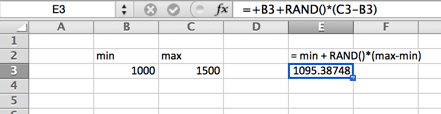
Distribution normale (Gaussienne)

C’est aussi votre courbe standard en forme de cloche. Cette formule de simulation de Monte Carlo se caractérise par une répartition uniforme de chaque côté (la médiane et la moyenne sont les mêmes – et aucune asymétrie). Les queues de la courbe vont à l’infini. Ce n’est donc peut-être pas la courbe idéale pour les prix des maisons, où quelques maisons haut de gamme augmentent la moyenne (moyenne) bien au-dessus de la médiane, ou dans les cas où il y a un minimum ou un maximum difficile. Un exemple de ceci peut être le salaire minimum dans votre région. Veuillez noter que le nom de la fonction varie en fonction de votre version.

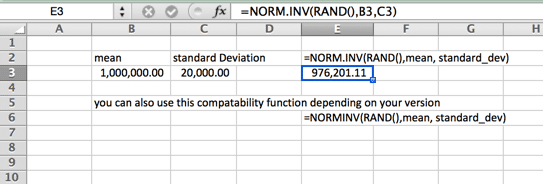
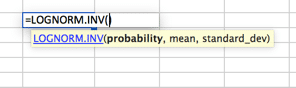
Distribution lognormale

Distribution où le logarithme est normalement distribué avec la moyenne et l’écart type. La configuration est donc similaire à la distribution normale, mais veuillez noter que les variables mean et standard_dev sont censées représenter le logarithme.

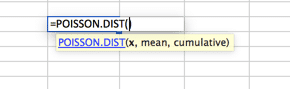
Distribution de poisson

C’est probablement la distribution la plus sous-utilisée. Par défaut, de nombreuses personnes utilisent une courbe de distribution normale lorsque Poisson convient mieux à leurs modèles. Poisson est mieux décrit lorsqu’il y a une grande distribution vers le tout début qui se dissipe rapidement pour former une longue queue d’un côté. Un exemple de ceci serait un centre d’appels, où aucun appel n’est répondu avant le deuxième ZÉRO. Suivi de la majorité des appels répondus dans les 2 premiers intervalles (disons 30 et 60 secondes) avec une baisse rapide du volume et une longue queue, avec très peu d’appels répondus en 20 minutes (prétendument).

Le but ici n’est pas de vous montrer toutes les distributions possibles dans Excel, car cela sort du cadre de cet article. Plutôt pour vous assurer que vous savez qu’il existe de nombreuses options disponibles pour votre simulation Monte Carlo. Ne tombez pas dans le piège de supposer qu’une courbe de distribution normale convient à toutes vos modélisations de données. Pour trouver plus de courbes, allez dans les fonctions statistiques de votre classeur Excel et étudiez. Si vous avez des questions, posez-les dans la section commentaires ci-dessous.

Construire le Modèle

Pour cette configuration, nous supposerons une distribution normale et 1 000 itérations.

Variables d’entrée

La configuration suppose une distribution normale. Une distribution normale nécessite trois variables; probabilité, moyenne et écart-type. Nous aborderons la moyenne et l’écart type dans notre première étape. Je suppose un problème de prévision financière qui se compose de Revenus, de Dépenses variables et fixes. Où les Revenus moins les Dépenses Variables moins les Dépenses Fixes sont égaux aux Bénéfices. Les dépenses fixes sont des coûts irrécupérables des installations et de l’équipement, de sorte qu’aucune courbe de répartition n’est supposée. Les courbes de répartition sont supposées pour les Produits et les Charges variables.

Première simulation

L’exemple ci-dessous indique les paramètres de revenu. La formule peut être copiée et collée dans la cellule D6 pour les dépenses variables. Pour les revenus et les dépenses, nous vous la norme de fonction.INV() où les paramètres sont:

• Probabilité = la fonction RAND() pour obtenir un nombre aléatoire basé sur les autres critères de la distribution.
• Moyenne = La moyenne utilisée à l’étape 1. Pour les revenus, c’est C3.
• Écart type = L’écart type utilisé à l’étape 1. Pour les revenus, c’est C4

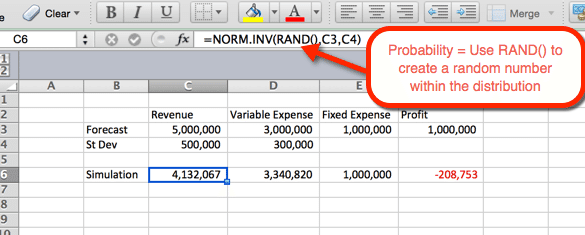
Puisque RAND() est utilisé comme probabilité, une probabilité aléatoire est générée lors de l’actualisation. Nous utiliserons cela à notre avantage à l’étape suivante.

1 000 Simulations

Il existe plusieurs façons de faire 1 000 variations ou plus. L’option la plus simple consiste à prendre la formule de l’étape #2 et à la rendre absolue. Ensuite, copiez et collez 1 000 fois. C’est simple, mais pas très chic. Et si Ferris Bueller peut sauver le monde en montrant un nouveau jeu de Tic Tac Toe à un ordinateur, alors nous pouvons également pimenter cette analyse. Aventurons-nous dans le monde des tables.

• Nous voulons d’abord créer un contour pour une table. Pour ce faire, nous listons les nombres de 1 à 1 000 en lignes. Dans l’exemple d’image ci-dessous, la liste des numéros commence par B12.
• dans la colonne suivante, dans la cellule C12, nous référencerons la première itération.

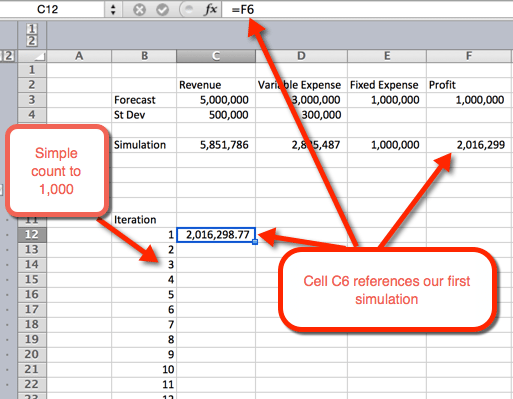
• Ensuite, mettez en surbrillance la zone où nous voulons héberger les 1 000 itérations
• Sélectionnez Data > Tables de données
• Pour la cellule d’entrée de colonne: Sélectionnez une cellule vide. Dans le fichier de téléchargement, la cellule D11 est sélectionnée
• Sélectionnez OK

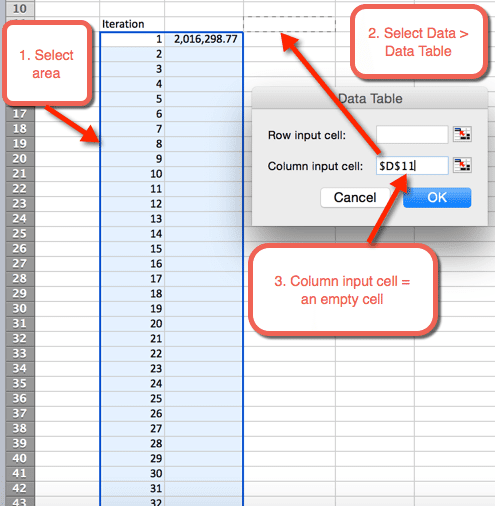
• Une fois que OK est sélectionné à l’étape précédente, une table est insérée qui remplit automatiquement les 1 000 simulations

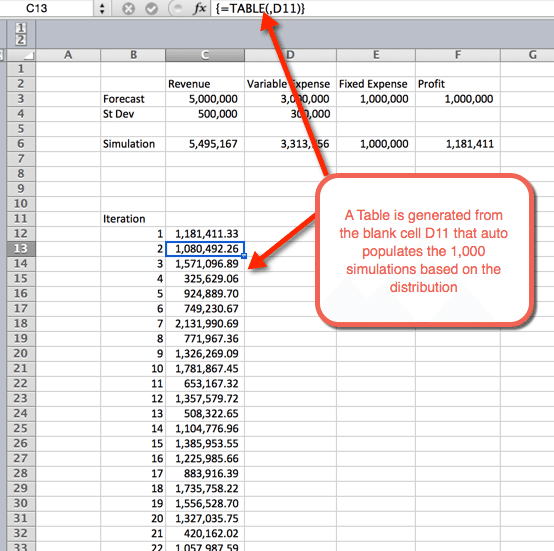
Statistiques sommaires

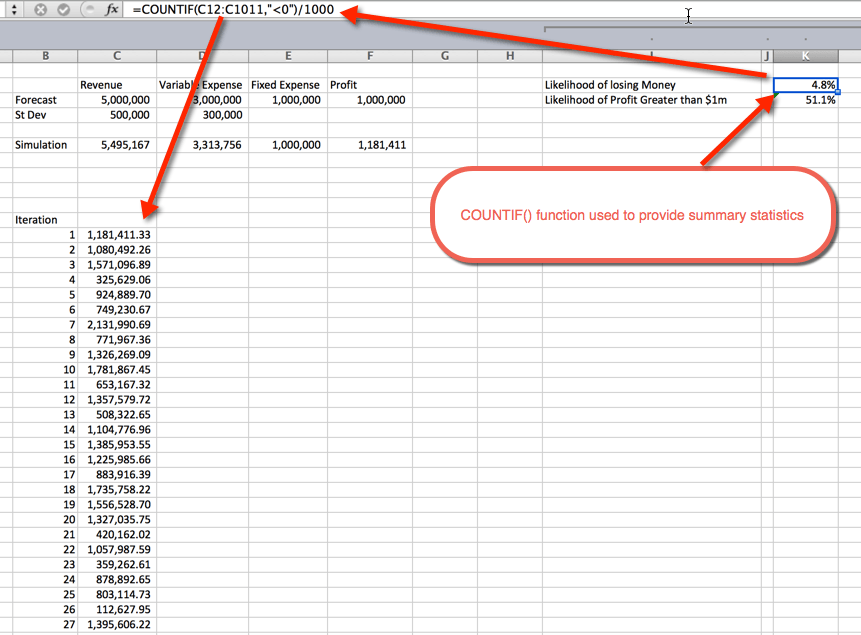
Une fois les simulations exécutées, il est temps de rassembler des statistiques sommaires. Cela peut être fait de plusieurs façons. Dans cet exemple, j’ai utilisé la fonction COUNTIF() pour déterminer le pourcentage de simulations non rentables et la probabilité d’un bénéfice supérieur à 1 million de dollars. Comme prévu, la probabilité de plus de 1 million de dollars oscille autour de 50%. En effet, nous avons utilisé des courbes de distribution normales qui sont réparties uniformément autour de la moyenne, qui était de 1 million de dollars. La probabilité de perdre de l’argent est de 4,8%. Cela a été recueilli en utilisant la fonction COUNTIF() pour compter les simulations inférieures à zéro et en divisant par les 1 000 itérations totales.

Télécharger

Dans la vidéo ci-dessus, Oz s’interroge sur les différentes utilisations de la Simulation de Monte Carlo. Pourquoi l’avez-vous utilisé? Y a-t-il des exemples spécifiques que vous pouvez partager avec le groupe ? Si c’est le cas, laissez une note ci-dessous dans la section commentaires. Aussi, n’hésitez pas à vous inscrire à notre newsletter, afin que vous puissiez rester à jour comme nouveau Excel.TV les spectacles sont annoncés. Laissez-moi un message ci-dessous pour rester en contact.