Was ist Monte Carlo Simulation?

Die Monte-Carlo-Simulation ist ein Prozess, bei dem Wahrscheinlichkeitskurven verwendet werden, um die Wahrscheinlichkeit eines Ergebnisses zu bestimmen. Sie können sich hier am Kopf kratzen und sagen… „Hey Rick, eine Verteilungskurve hat eine Reihe von Werten. Wie genau bestimme ich die Wahrscheinlichkeit eines Ergebnisses?“ Und noch besser, wie mache ich das in Microsoft Excel ohne spezielle Add-insThought würden Sie nie fragen.Dies geschieht, indem die Simulation tausende Male ausgeführt und die Verteilung der Ausgabe analysiert wird. Dies ist besonders wichtig, wenn Sie die Ausgabe mehrerer Verteilungskurven analysieren, die ineinander übergehen.Beispiel:

• Die Anzahl der verkauften Einheiten kann eine Verteilungskurve
• multipliziert mit dem Marktpreis haben, die eine andere Verteilungskurve haben kann
• minus variable Löhne, die eine andere Kurve haben
• usw., etc.

Sobald alle diese Verteilungen vermischt sind, kann die Ausgabe sehr komplex sein. Das Ausführen von Tausenden von Iterationen (oder Simulationen) dieser Kurven kann Ihnen einige Einblicke geben. Dies ist besonders nützlich bei der Analyse potenzieller Risiken für eine Entscheidung.

Monte Carlo beschreiben

Bei der Beschreibung der Monte-Carlo-Simulation beziehe ich mich oft auf den Film War Games aus den 1980er Jahren, in dem ein junger Mathew Broderick (vor Ferris Bueller) ein Hacker ist, der sein DFÜ-Modem verwendet, um sich in die Pentagon-Computer zu hacken und den 3. Weltkrieg zu starten. Irgendwie. Dann ließ er die Pentagon-Computer viele Simulationen der Tic Tac Toe-Spiele durchführen, um dem Computer beizubringen, dass niemand einen Atomkrieg führen wird – und dabei die Welt zu retten.Danke Ferris. Du bist ein Held.Hier ist ein Blick auf den Film, um Ihnen Big Time Monte Carlo in Aktion zu zeigen. Ich gehe davon aus, dass Sie die Politik übersehen werden, der unbeholfene Mann umarmt und natürlich, Dabney Coleman.

Verteilungskurven

Es gibt verschiedene Verteilungskurven, mit denen Sie Ihre Monte-Carlo-Simulation einrichten können. Und diese Kurven können basierend auf der Variablen ausgetauscht werden. Microsoft hat keine Formel namens „Monte Carlo Simulation durchführen“ in der Menüleiste 🙂

Gleichmäßige Verteilung

In einer gleichmäßigen Verteilung liegt die Wahrscheinlichkeit irgendwo zwischen dem Minimum und einem Maximum. Eine gleichmäßige Verteilung sieht aus wie ein Rechteck.

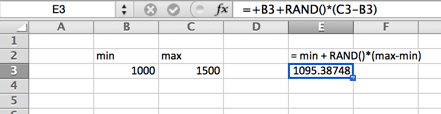
Normale (Gaußsche) Verteilung

Dies ist auch Ihre standardmäßige glockenförmige Kurve. Diese Monte-Carlo-Simulationsformel zeichnet sich dadurch aus, dass sie auf jeder Seite gleichmäßig verteilt ist (Median und Mittelwert sind gleich – und keine Schiefe). Die Schwänze der Kurve gehen bis ins Unendliche. Dies ist also möglicherweise nicht die ideale Kurve für Hauspreise, bei denen einige Top-End-Häuser den Durchschnitt (Mittelwert) deutlich über den Median erhöhen oder in Fällen, in denen es ein hartes Minimum oder Maximum gibt. Ein Beispiel hierfür kann der Mindestlohn in Ihrem Gebietsschema sein. Bitte beachten Sie, dass der Name der Funktion je nach Version variiert.

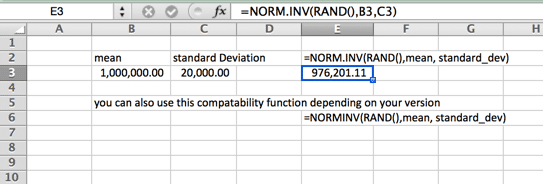
Lognormalverteilung

Eine Verteilung, bei der der Logarithmus normal mit dem Mittelwert und der Standardabweichung verteilt ist. Das Setup ähnelt also der Normalverteilung, aber bitte beachten Sie, dass die Variablen mean und standard_dev den Logarithmus darstellen sollen.

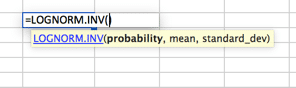
Poisson-Verteilung

Dies ist wahrscheinlich die am wenigsten ausgelastete Verteilung. Standardmäßig verwenden viele Benutzer eine Normalverteilungskurve, wenn Poisson besser zu ihren Modellen passt. Poisson wird am besten beschrieben, wenn es in der Nähe des Anfangs eine große Verteilung gibt, die sich schnell zu einem langen Schwanz auf einer Seite auflöst. Ein Beispiel hierfür wäre ein Callcenter, in dem keine Anrufe vor der zweiten NULL beantwortet werden. Gefolgt von der Mehrheit der Anrufe, die in den ersten 2 Intervallen beantwortet wurden (z. B. 30 und 60 Sekunden), mit einem schnellen Abfall der Lautstärke und einem langen Schwanz, wobei nur sehr wenige Anrufe in 20 Minuten beantwortet wurden (angeblich).

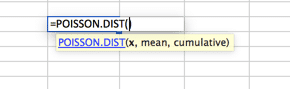
Der Zweck hier ist nicht, Ihnen jede mögliche Verteilung in Excel zu zeigen, da dies außerhalb des Umfangs dieses Artikels liegt. Vielmehr, um sicherzustellen, dass Sie wissen, dass es viele Optionen für Ihre Monte-Carlo-Simulation gibt. Tappen Sie nicht in die Falle, anzunehmen, dass eine Normalverteilungskurve für Ihre gesamte Datenmodellierung geeignet ist. Um weitere Kurven zu finden, gehen Sie die statistischen Funktionen in Ihrer Excel-Arbeitsmappe und untersuchen. Wenn Sie Fragen haben, stellen Sie sie in den Kommentaren unten.

Erstellen des Modells

Für diesen Aufbau nehmen wir eine Normalverteilung und 1.000 Iterationen an.

Eingangsvariablen

Das Setup geht von einer Normalverteilung aus. Eine Normalverteilung erfordert drei Variablen; Wahrscheinlichkeit, Mittelwert und Standardabweichung. Wir werden den Mittelwert und die Standardabweichung in unserem ersten Schritt angehen. Ich gehe von einem Finanzprognoseproblem aus, das aus Einnahmen, variablen und festen Ausgaben besteht. Wobei Umsatz abzüglich variabler Aufwendungen abzüglich fixer Aufwendungen gleich Gewinn ist. Die Fixkosten sind versunkene Kosten in Anlagen und Anlagen, so dass keine Verteilungskurve angenommen wird. Für Erlöse und variable Aufwendungen werden Verteilungskurven angenommen.

Erste Simulation

Das folgende Beispiel zeigt die Einstellungen für den Umsatz. Die Formel kann für variable Ausgaben kopiert und in Zelle D6 eingefügt werden. Für Einnahmen und Ausgaben verwenden wir die Funktionsnorm.INV() wobei die Parameter sind:

• Wahrscheinlichkeit = die Funktion RAND(), um eine Zufallszahl basierend auf den anderen Kriterien innerhalb der Verteilung zu erhalten.
• Mittelwert = Der im Schritt 1 verwendete Mittelwert. Für Einnahmen ist es C3.
• Standardabweichung = Die in Schritt 1 verwendete Standardabweichung. Für Einnahmen ist es C4

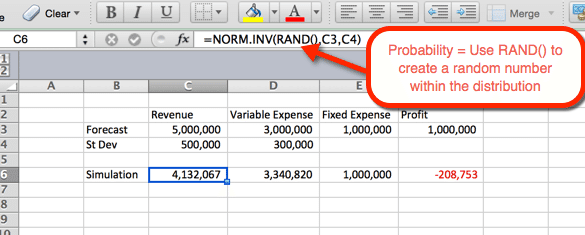
Da RAND() als Wahrscheinlichkeit verwendet wird, wird beim Refresh eine Zufallswahrscheinlichkeit generiert. Das werden wir im nächsten Schritt zu unserem Vorteil nutzen.

1.000 Simulationen

Es gibt mehrere Möglichkeiten, 1.000 oder mehr Variationen durchzuführen. Die einfachste Möglichkeit besteht darin, die Formel aus Schritt 2 zu nehmen und absolut zu machen. Dann kopieren und 1.000 mal einfügen. Das ist einfach, aber nicht sehr schick. Und wenn Ferris Bueller die Welt retten kann, indem er einem Computer ein neues Tic Tac Toe-Spiel zeigt, können wir diese Analyse auch aufpeppen. Wagen wir uns in die Welt der Tische.

• Zuerst wollen wir eine Gliederung für eine Tabelle erstellen. Wir tun dies, indem wir die Zahlen 1 bis 1.000 in Reihen auflisten. Im Beispielbild unten beginnt die Nummernliste in B12.
• In der nächsten Spalte in Zelle C12 verweisen wir auf die erste Iteration.

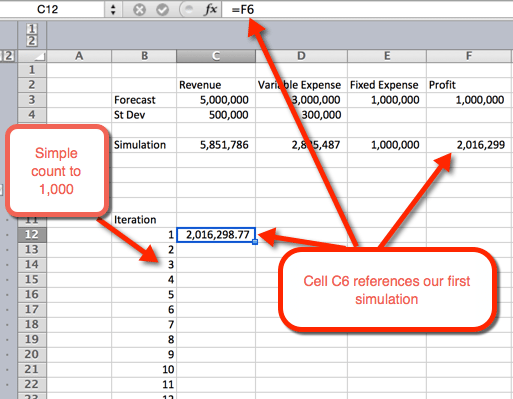
• Markieren Sie als nächstes den Bereich, in dem die 1.000 Iterationen untergebracht werden sollen
• Daten auswählen > Datentabellen
• Für Spalteneingabezelle: Wählen Sie eine leere Zelle aus. In der Download-Datei ist Zelle D11 ausgewählt
• Wählen Sie OK

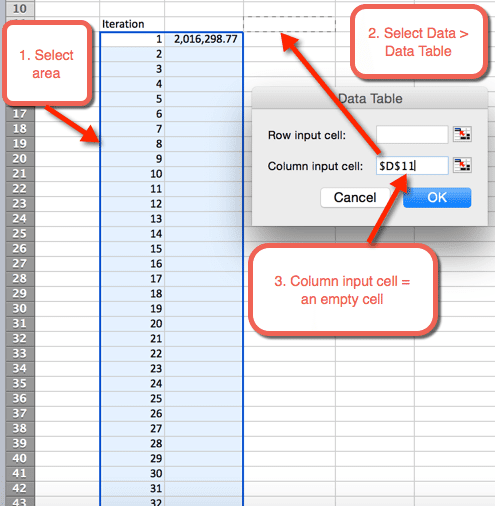
• Sobald OK aus dem vorherigen Schritt ausgewählt wurde, wird eine Tabelle eingefügt, die die 1.000 Simulationen automatisch auffüllt

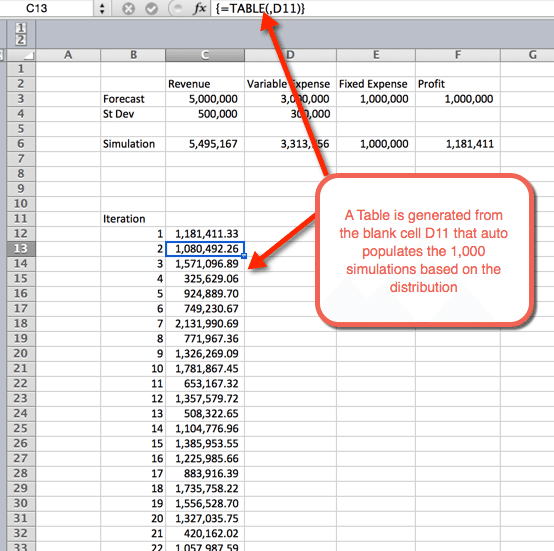
Zusammenfassende Statistiken

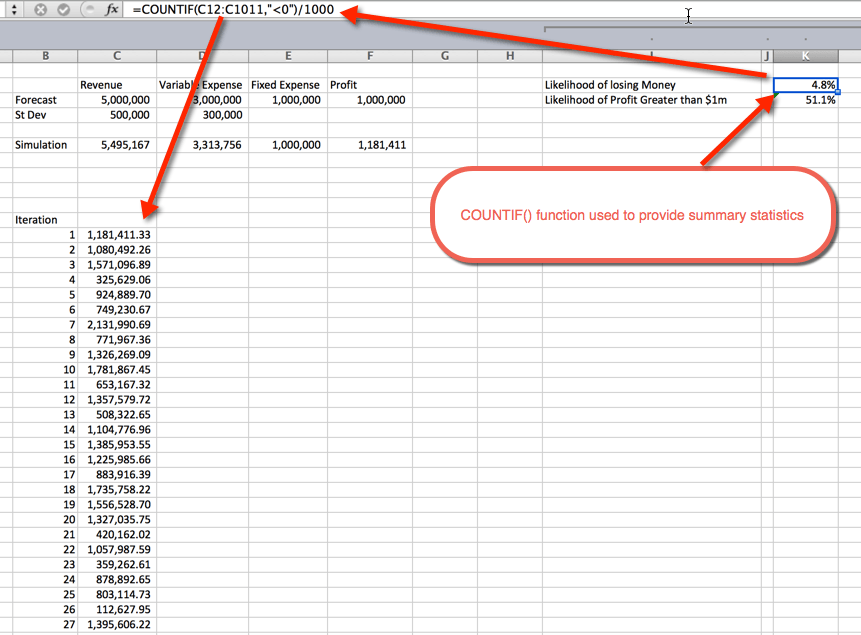
Sobald die Simulationen ausgeführt wurden, ist es an der Zeit, zusammenfassende Statistiken zu sammeln. Dies kann auf verschiedene Arten erfolgen. In diesem Beispiel habe ich die Funktion COUNTIF () verwendet, um den Prozentsatz der unrentablen Simulationen und die Wahrscheinlichkeit eines Gewinns von mehr als 1 Million US-Dollar zu bestimmen. Wie erwartet, die Wahrscheinlichkeit von mehr als $ 1M schwebt um 50%. Dies liegt daran, dass wir Normalverteilungskurven verwendet haben, die gleichmäßig um den Mittelwert verteilt sind, der $ 1M betrug. Die Wahrscheinlichkeit, Geld zu verlieren, beträgt 4,8%. Dies wurde mithilfe der Funktion COUNTIF () ermittelt, um die Simulationen zu zählen, die kleiner als Null waren, und durch die 1.000 Gesamtiterationen zu dividieren.

Holen Sie sich den Download

Im obigen Video fragt Oz nach den verschiedenen Verwendungsmöglichkeiten der Monte-Carlo-Simulation. Wofür hast du es benutzt? Gibt es konkrete Beispiele, die Sie mit der Gruppe teilen können? Wenn ja, hinterlassen Sie eine Notiz unten im Kommentarbereich. Melden Sie sich auch gerne für unseren Newsletter an, damit Sie als Neuling auf dem Laufenden bleiben Excel.TV shows sind angekündigt. Hinterlassen Sie mir unten eine Nachricht, um in Kontakt zu bleiben.

zu teilen