Vad är Monte Carlo simulering?

Monte Carlo-simulering är en process för att använda sannolikhetskurvor för att bestämma sannolikheten för ett resultat. Du kan skrapa huvudet här och säga… ”Hej Rick, en distributionskurva har en rad värden. Så hur exakt bestämmer jag sannolikheten för ett resultat?”Och ännu bättre, hur gör jag det i Microsoft Excel utan några speciella tillägg som du aldrig skulle fråga.Detta görs genom att köra simuleringen tusentals gånger och analysera fördelningen av utgången. Detta är särskilt viktigt när du analyserar utsignalen från flera fördelningskurvor som matas in i varandra.Exempel:

• # av sålda enheter kan ha en distributionskurva
• multiplicerat med marknadspris, vilket kan ha en annan distributionskurva
• minus rörliga löner som har en annan kurva
• etc., osv.

när alla dessa fördelningar blandas kan utmatningen vara ganska komplex. Att köra tusentals iterationer (eller simuleringar) av denna kurva kan ge dig några insikter. Detta är särskilt användbart vid analys av potentiell risk för ett beslut.

beskriv Monte Carlo

när jag beskriver Monte Carlo-simulering hänvisar jag ofta till 1980-talets film War Games, där en ung Mathew Broderick (före Ferris Bueller) är en hacker som använder sitt uppringda modem för att hacka in i Pentagon-datorerna och starta världskriget 3. Slags. Han fick sedan Pentagon-datorerna att göra många simuleringar av spelen Tic Tac Toe för att lära datorn att ingen kommer att göra ett kärnvapenkrig – och rädda världen i processen.Tack Ferris. Du är en hjälte.Här är en glimt av filmen för att visa dig Big time Monte Carlo i aktion. Jag antar att du kommer att förbise politiken, den besvärliga mannen som kramar och naturligtvis Dabney Coleman.

Distributionskurvor

det finns olika distributionskurvor som du kan använda för att ställa in din Monte Carlo-simulering. Och dessa kurvor kan bytas ut baserat på variabeln. Microsoft har inte en formel som heter” Do Monte Carlo Simulation ” i menyraden 🙂

enhetlig fördelning

i en enhetlig fördelning finns det lika sannolikhet någonstans mellan minimum och maximum. En enhetlig fördelning ser ut som en rektangel.

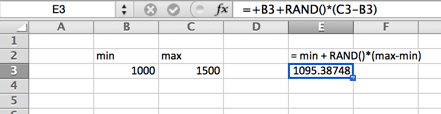
Normal (Gaussisk) fördelning

Detta är också din standard klockformade kurva. Denna Monte Carlo-Simuleringsformel kännetecknas av att den är jämnt fördelad på varje sida (median och medelvärdet är detsamma – och ingen skevhet). Kurvans svansar går vidare till oändligheten. Så det här kanske inte är den perfekta kurvan för huspriser, där några översta hus ökar genomsnittet (medelvärdet) långt över medianen, eller i fall där det finns ett hårt minimum eller maximalt. Ett exempel på detta kan vara minimilönen i ditt land. Observera att namnet på funktionen varierar beroende på din version.

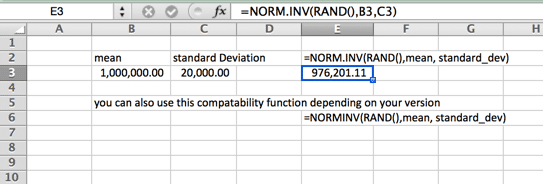
Lognormal Distribution

en distribution där logaritmen normalt distribueras med medelvärdet och standardavvikelsen. Så inställningen liknar normalfördelningen, men observera att medel-och standard_dev-variablerna är avsedda att representera logaritmen.

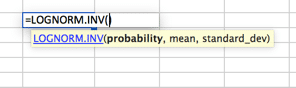
Poisson Distribution

detta är sannolikt den mest underutnyttjade distributionen. Som standard använder många en normalfördelningskurva när Poisson passar bättre för sina modeller. Poisson beskrivs bäst när det finns en stor fördelning nära början som snabbt försvinner till en lång svans på ena sidan. Ett exempel på detta skulle vara ett callcenter, där inga samtal besvaras före andra noll. Följt av de flesta samtal som besvarades under de första 2 intervallen (säg 30 och 60 sekunder) med en snabb nedgång i volym och en lång svans, med mycket få samtal besvarade på 20 minuter (påstås).

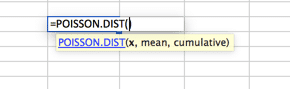
syftet här är inte att visa dig alla möjliga distributioner i Excel, eftersom det ligger utanför ramen för denna artikel. Snarare för att se till att du vet att det finns många alternativ för din Monte Carlo-simulering. Fall inte i fällan att anta att en normalfördelningskurva passar rätt för all din datamodellering. För att hitta fler kurvor, gå till de statistiska funktionerna i din Excel-arbetsbok och undersöka. Om du har frågor, Ställ dem i kommentarfältet nedan.

bygga modellen

för denna uppsättning kommer vi att anta en normalfördelning och 1000 iterationer.

inmatningsvariabler

inställningen förutsätter en normalfördelning. En normalfördelning kräver tre variabler; Sannolikhet, medelvärde och standardavvikelse. Vi kommer att ta itu med medelvärdet och standardavvikelsen i vårt första steg. Jag antar ett finansprognosproblem som består av intäkter, rörliga och fasta kostnader. Där intäkter minus rörliga kostnader minus fasta kostnader är lika med vinst. De fasta kostnaderna är sjunkna kostnader i anläggningar och utrustning, så ingen distributionskurva antas. Fördelningskurvor antas för intäkter och rörliga kostnader.

första simuleringen

exemplet nedan anger inställningarna för intäkter. Formeln kan kopieras och klistras in i cell D6 för rörliga kostnader. För intäkter och kostnader vi du funktionen NORM.Inv() där parametrarna är:

• Sannolikhet = funktionen RAND () för att framkalla ett slumptal baserat på de andra kriterierna inom fördelningen.
• medelvärde = medelvärdet som används i steg 1. För intäkter är det C3.
• standardavvikelse = standardavvikelsen som används i steg 1. För intäkter är det C4

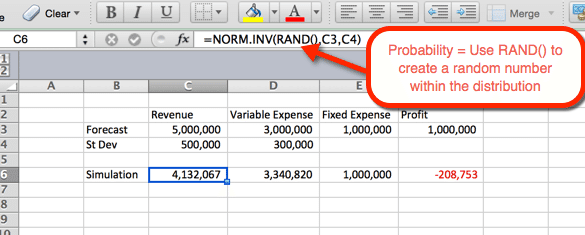
eftersom RAND () används som Sannolikhet genereras en slumpmässig Sannolikhet vid uppdatering. Vi kommer att använda detta till vår fördel i nästa steg.

1000 simuleringar

det finns flera sätt att göra 1000 eller fler variationer. Det enklaste alternativet är att ta formeln från steg #2 och göra den absolut. Kopiera och klistra in 1000 gånger. Det är enkelt, men inte särskilt snyggt. Och om Ferris Bueller kan rädda världen genom att visa ett nytt Tic Tac Toe-spel till en dator, så kan vi också krydda denna analys. Låt oss ge oss in i världen av tabeller.

• först vill vi skapa en kontur för en tabell. Vi gör detta genom att lista siffrorna 1 till 1000 i rader. I exempelbilden nedan börjar nummerlistan i B12.
• i nästa kolumn, i cell C12, kommer vi att referera till den första iterationen.

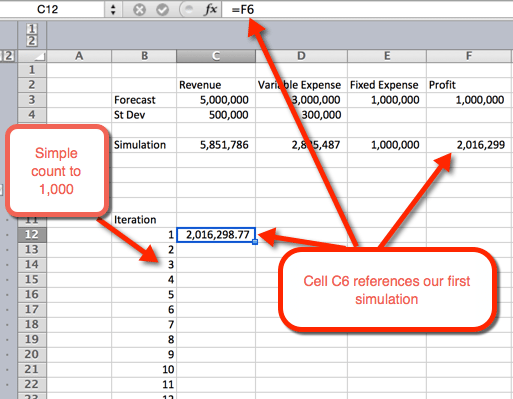
• nästa markera det område där vi vill hysa de 1000 iterationerna
• Välj Data > datatabeller
• för Kolumninmatningscell: välj en tom cell. I nedladdningsfilen väljs cell D11
• välj OK

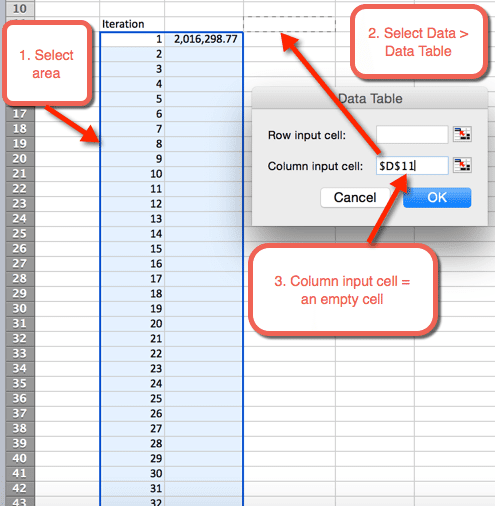
• när OK har valts från föregående steg infogas en tabell som autopopulerar de 1000 simuleringarna

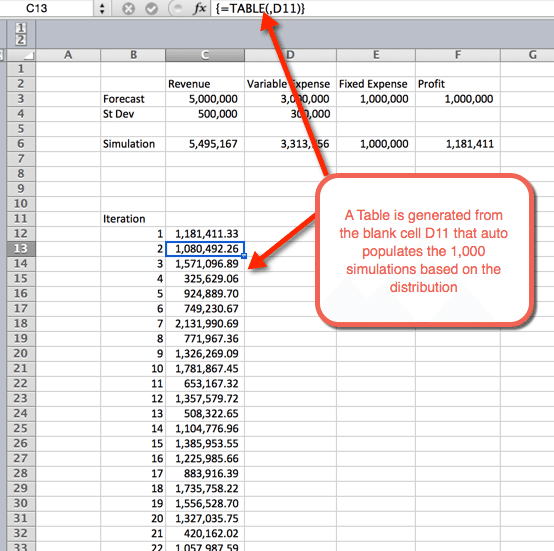
sammanfattande statistik

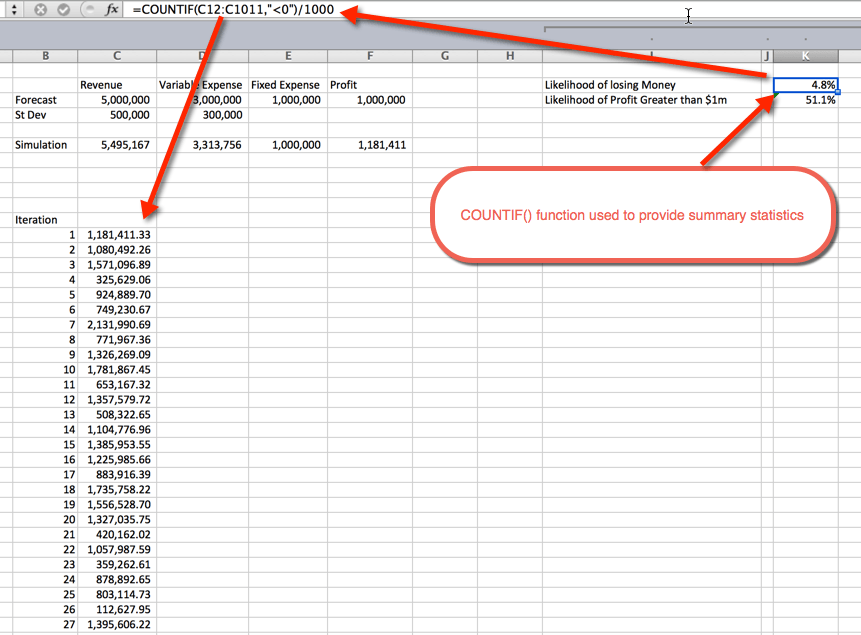
när simuleringarna har körts är det dags att samla in sammanfattande statistik. Detta kan göras på flera sätt. I det här exemplet använde jag COUNTIF () – funktionen för att bestämma andelen simuleringar som är olönsamma och sannolikheten för en vinst större än 1 miljon dollar. Som förväntat ligger sannolikheten för större än $1m runt 50%. Detta beror på att vi använde normalfördelningskurvor som är jämnt fördelade runt medelvärdet, vilket var $1m.sannolikheten att förlora pengar är 4.8%. Detta samlades genom att använda COUNTIF () – funktionen för att räkna simuleringarna som var mindre än noll och dividerade med de 1000 totala iterationerna.

hämta nedladdningen

i videon ovan frågar Oz om de olika användningarna för Monte Carlo-simulering. Vad har du använt den till? Finns det några specifika exempel som du kan dela med gruppen? Om så är fallet, lämna en anteckning nedan i kommentarfältet. Också, gärna registrera dig för vårt nyhetsbrev, så att du kan hålla dig uppdaterad som ny Excel.TV utställningar tillkännages. Lämna mig ett meddelande nedan för att hålla kontakten.