Innehållsförteckning
- luftbränsleförhållande definition
- luftbränsleförhållande formel
- luftbränsleförhållande för olika bränslen
- hur stökiometrisk luftbränsleförhållande beräknas
- Lambda luftbränsleförhållande
- luftbränsleförhållande och motorprestanda
- kalkylator för luftbränsleförhållande
- påverkan av luftbränsleförhållande på motorutsläpp
- Lambda förbränningskontroll med sluten slinga
definition av luftbränsleförhållande
termiska motorer använder bränsle och syre (från luft) för att producera energi genom förbränning. För att garantera förbränningsprocessen måste vissa mängder bränsle och luft tillföras i förbränningskammaren. En fullständig förbränning sker när allt bränsle brinner, i avgaserna kommer det inte att finnas några mängder oförbränt bränsle.
luftbränsleförhållandet definieras som förhållandet mellan luft och bränsle i en blandning beredd för förbränning. Om vi till exempel har en blandning av metan och luft som har luftbränsleförhållandet 17, 5 betyder det att vi i blandningen har 17, 5 kg luft och 1 kg metan.
det ideala (teoretiska) luftbränsleförhållandet, för en fullständig förbränning, kallas stökiometrisk luftbränsleförhållande. För en bensinmotor (bensin) är det stökiometriska luftbränsleförhållandet cirka 14,7: 1. Det betyder att vi behöver 14,7 kg luft för att bränna helt 1 kg bränsle. Förbränningen är möjlig även om AFR är annorlunda än stökiometrisk. För att förbränningsprocessen ska äga rum i en bensinmotor är minsta AFR cirka 6:1 och maximalt kan gå upp till 20:1.
när luftbränsleförhållandet är högre än det stökiometriska förhållandet kallas luftbränsleblandningen mager. När luftbränsleförhållandet är lägre än det stökiometriska förhållandet kallas luftbränsleblandningen rik. Till exempel, för en bensinmotor är en AFR på 16,5:1 mager och 13,7:1 rik.
gå tillbaka
formel för luftbränsleförhållande
i samband med förbränningsmotorer definieras luftbränsleförhållandet (AF eller AFR) som förhållandet mellan massan av luftma och massbränsle MF, som används av motorn när den körs:
\ {AFR = \ frac{m_a}{m_f}} \ tag{1}\]
det inversa förhållandet kallas bränsle-luftförhållande (FA eller FAR) och det beräknas som:
\
gå tillbaka
luftbränsleförhållande för olika bränslen
i tabellen nedan kan vi se det stökiometriska luftbränsleförhållandet för flera fossila bränslen.
| bränsle | Kemisk formel | AFR |
| metanol | CH3OH | 6.47:1 |
| etanol | C2H5OH | 9:1 |
| Butanol | C4H9OH | 11, 2:1 |
| Diesel | C12H23 | 14.5:1 |
| bensin | C8H18 | 14.7:1 |
| propan | C3H8 | 15.67:1 |
| metan | CH4 | 17.19:1 |
| väte | H2 | 34.3:1 |
källa: wikipedia.org
till exempel, för att bränna helt 1 kg etanol behöver vi 9 kg luft och för att bränna 1 kg dieselbränsle behöver vi 14, 5 kg luft.
gnisttändningsmotorer (si) körs vanligtvis på bensin (bensin) bränsle. AFR för SI-motorerna varierar inom intervallet 12:1 (rich) till 20: 1 (lean), beroende på motorns driftsförhållande (temperatur, hastighet, belastning etc.). Moderna förbränningsmotorer arbetar så mycket som möjligt runt den stökiometriska AFR (främst av gasefterbehandlingsskäl). I tabellen nedan kan du se ett exempel på en si-motor AFR, funktion av motorvarvtal och vridmoment.
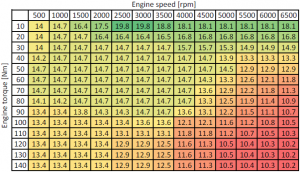
bild: Exempel på AFR-funktion (air fuel ratio) för motorvarvtal och vridmoment
motorer med kompressionständning (ci) körs vanligtvis på dieselbränsle. På grund av förbränningsprocessen körs CI-motorer alltid på magra blandningar, med AFR mellan 18:1 och 70:1. Huvudskillnaden jämfört med SI-motorer är att CI-motorer körs på stratifierade (icke homogena) luftbränsleblandningar, medan SI körs på homogena blandningar (vid portinjektionsmotorer).
tabellen ovan anges i ett Scilab-skript och en konturdiagram genereras.
EngSpd_rpm_X = ;EngTq_Nm_Y = ;EngAFR_rat_Z = ;contour(EngSpd_rpm_X,EngTq_Nm_Y,EngAFR_rat_Z',30)xgrid()xlabel('Engine speed ')ylabel('Engine torque ')title('x-engineer.org')
att köra Scilab-instruktionerna ovan genererar följande konturdiagram:

bild: Air fuel contour plot med Scilab
gå tillbaka
hur stökiometrisk luftbränsleförhållande beräknas
för att förstå hur det stökiometriska luftbränsleförhållandet beräknas måste vi titta på förbränningsprocessen för bränslet. Förbränning är i grunden en kemisk reaktion (kallad oxidation) där ett bränsle blandas med syre och producerar koldioxid (CO2), vatten (H2O) och energi (värme). Tänk på att för att oxidationsreaktionen ska inträffa behöver vi en aktiveringsenergi (gnista eller hög temperatur). Nettoreaktionen är också mycket exoterm (med värmefrisättning).
\{spark \ text {(SI)}} \text{koldioxid} + \text{vatten} + \text{energi}\]
exempel 1. För en bättre förståelse, låt oss titta på oxidationsreaktionen av metan. Detta är en ganska vanlig kemisk reaktion, eftersom metan är den primära komponenten i naturgas (i proportion av cirka 94 %).
Steg 1. Skriv den kemiska reaktionen (oxidation)
\
steg 2. Balansera ekvationen
\
steg 3. Skriv ner standard atomvikt för varje atom
\
steg 4. Beräkna massan av bränsle, som är 1 mol metan, bestående av 1 atom kol och 4 atomer väte.
\
Steg 5. Beräkna syrgasmassan, som består av 2 mol, varje mol består av 2 syreatomer.
\
steg 6. Beräkna den nödvändiga luftmassan som innehåller den beräknade syrgasmassan, med hänsyn till att luften innehåller cirka 21% syre.
\
Steg 7. Beräkna luftbränsleförhållandet med hjälp av ekvation (1)
\
den beräknade AFR för metan är inte exakt som anges i litteraturen. Skillnaden kan komma från det faktum att vi i vårt exempel gjorde flera antaganden (luft innehåller bara 21% syre, förbränningsprodukterna är bara koldioxid och vatten).
exempel 2. Samma metod kan tillämpas för förbränning av bensin. Med tanke på att bensin består av iso-oktan (C8H18), beräkna det stökiometriska luftbränsleförhållandet för bensin.
Steg 1. Skriv den kemiska reaktionen (oxidation)
\
steg 2. Balansera ekvationen
\
steg 3. Skriv ner standard atomvikt för varje atom
\
steg 4. Beräkna massan av bränsle, som är 1 mol iso-oktan, bestående av 8 atomer kol och 18 atomer väte.
\
Steg 5. Beräkna syrgasmassan, som består av 12,5 mol, varje mol består av 2 syreatomer.
\
steg 6. Beräkna den nödvändiga luftmassan som innehåller den beräknade syrgasmassan, med hänsyn till att luften innehåller cirka 21% syre.
\
Steg 7. Beräkna luftbränsleförhållandet med hjälp av ekvation (1)
\
återigen är det beräknade stökiometriska luftbränsleförhållandet för bensin något annorlunda än det som anges i litteraturen. Således är resultatet acceptabelt eftersom vi gjorde många antaganden (bensin innehåller endast iso-oktan, luft innehåller endast syre i proportion av 21 %, de enda förbränningsprodukterna är koldioxid och vatten, förbränningen är idealisk).
gå tillbaka
Lambda luftbränsleförhållande
vi har sett vad som är och hur man beräknar det stökiometriska (ideala) luftbränsleförhållandet. I verkligheten fungerar förbränningsmotorer inte exakt med ideal AFR, utan med värden nära den. Därför har vi ett idealiskt och ett faktiskt AFR-förhållande för luftbränsle. Förhållandet mellan det faktiska luftbränsleförhållandet (AFRactual) och det ideala/stökiometriska luftbränsleförhållandet (AFRideal) kallas ekvivalensluftbränsleförhållandet eller lambda (kg).
\{\lambda = \ frac{AFR_{actual}}{AFR_ {ideal}}} \tag{3}\]
till exempel är det ideala luftbränsleförhållandet för en bensinmotor 14,7:1. Om den faktiska / verkliga AFR är 13,5 kommer ekvivalensfaktorn lambda att vara:
\
beroende på värdet på lambda, berättas motorn att arbeta med mager, stökiometrisk eller rik luftbränsleblandning.
| Likvärdighet faktor | Luft-bränsle blandning typ | Beskrivning |
| λ < 1.00 | Rikt | Det finns inte tillräckligt med luft för att brinna helt mängden bränsle; efter förbränning det är oförbränt bränsle i avgaserna |
| λ = 1.00 | Stökiometriska (ideal) | massan av luften är exakt för en fullständig förbränning av bränslet, efter förbränning finns det inget överskott av syre i avgaserna och inget oförbränt bränsle |
| λ > 1.00 | Lean | Det är mer syre än vad som krävs för att bränna helt mängden bränsle; efter förbränning finns det överskott av syre i avgaserna |
beroende på typ av bränsle (bensin eller diesel) och typ av injektion (direkt eller indirekt) kan en förbränningsmotor fungera med magra, stökiometriska eller rika luftbränsleblandningar.

bild: Ecoboost 3-cylindrig bensinmotor med direktinsprutning (lambda-karta)
kredit: Ford
till exempel kör Ford Ecoboost 3-cylindrig motor med stökiometrisk luftbränsleförhållande för tomgång till medelvarvtal och komplett lastområde och med rik luftbränsleblandning vid hög hastighet och belastning. Anledningen till att den körs med rik blandning vid hög motorvarvtal och belastning är motorkylning. Det extra bränslet (som kommer att förbli oförbränt) injiceras för att absorbera värme (genom avdunstning), vilket minskar temperaturen i förbränningskammaren.

bild: dieselmotor (lambda karta)
kredit: wtz.de
en dieselmotor med kompressionständning (diesel) körs hela tiden med mager luftbränsleblandning, värdet på ekvivalensfaktorn (XXL) beroende på motorns driftpunkt (hastighet och vridmoment). Anledningen till detta är arbetsprincipen för en dieselmotor: styrning av lasten inte genom luftmassa (som alltid är överflödig) utan genom bränslemassa (injektionstid).
kom ihåg att en stökiometrisk ekvivalensfaktor (Xiaomi = 1,00) betyder ett luftbränsleförhållande på 14,7:1 för bensinmotorer och 14,5:1 för dieselmotorer.
gå tillbaka
luftbränsleförhållande och motorprestanda
motorns prestanda när det gäller effekt och bränsleförbrukning är mycket beroende av luftbränsleförhållandet. För en bensinmotor erhålls den lägsta bränsleförbrukningen vid mager AFR. Huvudskälet är att det finns tillräckligt med syre tillgängligt för att bränna helt allt bränsle som översätts i mekaniskt arbete. Å andra sidan erhålls maximal effekt med rika luftbränsleblandningar. Som förklarats tidigare, sätter mer bränsle i cylindern vid hög motorbelastning och hastighet, kyler ner förbränningskammaren (genom bränsleindunstning och värmeabsorption) vilket gör att motorn kan producera maximalt motorns vridmoment och därmed maximal effekt.

bild: motoreffekt och bränsleförbrukningsfunktion för luftbränsleförhållande (lambda)
i figuren ovan kan vi se att vi inte kan få maximal effekt på motorn och den lägsta bränsleförbrukningen med samma luftbränsleförhållande. Den lägsta bränsleförbrukningen (bästa bränsleekonomin) erhålls med magra luftbränsleblandningar, med en AFR på 15,4:1 och en ekvivalensfaktor (GHz) på 1,05. Den maximala motoreffekten produceras med rika luftbränsleblandningar, med en AFR på 12,6:1 och en ekvivalensfaktor (POV) på 0,86. Med en stökiometrisk luftbränsleblandning (XXL = 1) finns det en kompromiss mellan maximal motoreffekt och minimal bränsleförbrukning.
motorer med kompressionständning (diesel) körs alltid på magra luftbränsleblandningar(2456 > 1.00). De flesta av de moderna dieselmotorerna kör med GHz mellan 1,65 och 1,10. Den maximala effektiviteten (lägsta bränsleförbrukning) erhålls runt 2,65 xnumx xnumx. Att öka bränslemängden över detta värde (går mot 1.10) Kommer att producera mer sot (oförbrända bränslepartiklar).
det finns en intressant studie utförd av R. Douglas på 2-taktscykelmotorer. I sin doktorsavhandling ”Closed Cycle Studies of a Two-takts Cycle Engine” kommer R. Douglas med ett matematiskt uttryck för ekvivalensfaktorns förbränningseffektivitetsfunktion (GHz).
för gnisttändning (bensinmotor) med en ekvivalensfaktor mellan 0,80 och 1.20, förbränningseffektiviteten är:
\
för kompressionständning (dieselmotor) med en ekvivalensfaktor mellan 1,00 och 2,00, förbränningseffektiviteten är:
\
för dieselmotorer, om ekvivalensfaktorn går över 2,00, är förbränningseffektiviteten maximal (1,00 eller 100 %).
vi kan använda ett Scilab-skript för att plotta variationen i ekvivalensfaktorns förbränningseffektivitetsfunktion.
lmbd_g = ;lmbd_d = ;eff_lmbd_g = -1.6082+4.6509*lmbd_g-2.0746*lmbd_g.^2;eff_lmbd_d = -4.18+8.87*lmbd_d-5.14*lmbd_d.^2+lmbd_d.^3;plot(lmbd_g,eff_lmbd_g,'b','LineWidth',2)holdplot(lmbd_d,eff_lmbd_d,'r','LineWidth',2)xgrid()xlabel('$\lambda \text{ }$')ylabel('$\eta_{\lambda} \text{ }$')title('x-engineer.org')legend('gasoline','diesel',4)
köra Scilab instruktionerna ovan matar ut följande grafiska fönster.

bild: förbränningseffektivitet funktion ekvivalens faktor
som ni kan se, kompressionständning (diesel) motor, vid stökiometriska luftbränsleförhållandet har en mycket låg förbränningseffektivitet. Den bästa förbränningseffektiviteten erhålls vid 2,00 XNUMX för diesel och 1,12 XNUMX för gnisttändningsmotorer (bensin).
gå tillbaka
kalkylator för luftbränsleförhållande
| ma | bränsletyp beräkna |
|
| mf |
Observation: förbränningseffektiviteten beräknas endast för diesel-och bensinbränsle (bensin) med hjälp av ekvationerna (4) och (5). För de andra bränslena är beräkningen av förbränningseffektivitet inte tillgänglig (NA).
gå tillbaka
påverkan av luftbränsleförhållandet på motorutsläpp
förbränningsmotorns avgasutsläpp beror starkt på luftbränsleförhållandet (ekvivalensfaktor). De viktigaste avgasutsläppen i ICE sammanfattas i tabellen nedan.
| avgasutsläpp | beskrivning |
| CO | kolmonoxid |
| HC | kolväte |
| NOx | kväveoxider |
| sot | oförbrända bränslepartiklar |
för en bensinmotor påverkas CO -, HC-och NOx-avgasutsläppen starkt av luftbränsleförhållandet. CO och HC produceras huvudsakligen med rik luftbränsleblandning, medan NOx med magra blandningar. Så det finns ingen fast luftbränsleblandning för vilken vi kan få ett minimum för alla avgasutsläpp.

bild: Bensinmotorkatalysatoreffektivitetsfunktion för luftbränsleförhållande
en trevägs katalysator (TWC), som används för bensinmotorer, har den högsta effektiviteten när motorn arbetar i ett smalt band runt stökiometrisk luftbränsleförhållande. TWC omvandlar mellan 50 … 90% kolväten och 90 … 99% kolmonoxid och kväveoxider, när motorn går med GHz = 1,00.
gå tillbaka
Lambda förbränningskontroll med sluten slinga
för att uppfylla avgasutsläppsreglerna är det viktigt för förbränningsmotorer (särskilt bensin) att ha en exakt kontroll av luftbränsleförhållandet. Därför har alla moderna förbränningsmotorer sluten slinga för luftbränsleförhållande (lambda).

bild: Förbränningsmotor sluten slinga lambda kontroll (bensinmotorer)
- luftmassflödesgivare
- primär katalysator
- sekundär katalysator
- bränsleinsprutare
- uppströms lambda (syre) sensor
- nedströms lambda (syre) sensor
- bränsleförsörjningskrets
- insugningsgrenrör
- avgasgrenrör
den kritiska komponenten för att systemet ska fungera är Lambda-sensorn (syre). Denna sensor mäter nivån av syremolekyler i avgaserna och skickar informationen till motorns elektroniska styrenhet (ECU). Baserat på värdet av syresensoravläsningen justerar bensinmotorns ECU nivån på bränslemassan för att hålla luftbränsleförhållandet runt den stökiometriska nivån (XXL = 1,00).
till exempel (bensinmotorer), om nivån av syremolekyler ligger över tröskeln för stökiometrisk nivå (därför har vi en mager blandning), vid nästa injektionscykel, kommer den injicerade bränslemängden att ökas för att utnyttja överskottsluften. Tänk på att motorn alltid kommer att övergå från mager blandning till rik blandning mellan injektionscykler, vilket ger ett ”genomsnitt” av stökiometriska luftbränsleblandningar/förhållande.
för dieselmotorer, eftersom den alltid körs på magert luftbränsleförhållande, utförs lambda-kontrollen på ett annat sätt. Slutmålet är fortfarande detsamma, kontroll av avgasutsläppen.