Índice (Clique para pular para a seção):

1. Definição & Fórmula
2. Exemplo
3. Problemas com Interpretação
4. > Vantagens
5. Covariância no Excel

Definição & Fórmula

Covariância é uma medida da quantidade de duas variáveis aleatórias variam juntas. É semelhante à variância, mas onde a variância informa como uma única variável varia, a variância de co informa como duas variáveis variam juntas.

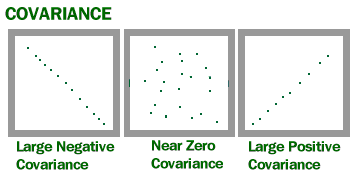
imagem de U de Wisconsin.

a fórmula de covariância

Assista ao vídeo para um exemplo:

não consegue ver o vídeo? Clicar.

a fórmula é:
Cov ( X, Y) = Σ e ((X – μ) E (Y – ν)) / n-1 onde:

• X é uma variável aleatória
• E(X) = μ é o valor esperado (média) da variável aleatória X e
• E(Y) = ν é o valor esperado (média) da variável aleatória Y
• n = o número de itens no conjunto de dados.
• Σ notação de soma.

Voltar ao início

Exemplo

Calcular a covariância para o seguinte conjunto de dados:
x: 2.1, 2.5, 3.6, 4.0 (média = 3.1)
y: 8, 10, 12, 14 (média = 11)

Substituir os valores na fórmula e resolver:
Cov(X,Y) = ΣE((X-µ)(Y-ν)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267

o resultado é positivo, o que significa que as variáveis estão positivamente relacionadas.

nota sobre a divisão por n ou n-1:
ao lidar com amostras, existem termos n – 1 que têm a liberdade de variar (ver: graus de liberdade). Se você está encontrando a covariância de apenas duas variáveis aleatórias, basta dividir por N.
voltar ao topo

problemas com interpretação

uma grande covariância pode significar uma forte relação entre variáveis. No entanto, você não pode comparar variações sobre conjuntos de dados com escalas diferentes (como libras e polegadas). Uma covariância fraca em um conjunto de dados pode ser forte em um conjunto de dados diferente com escalas diferentes.

o principal problema com a interpretação é que a ampla gama de resultados que ela assume dificulta a interpretação. Por exemplo, seu conjunto de dados pode retornar um valor de 3 ou 3.000. Essa ampla gama de valores é causada por um fato simples; Quanto maiores Os valores X e Y, maior a covariância. Um valor de 300 nos diz que as variáveis estão correlacionadas, mas ao contrário do coeficiente de correlação, esse número não nos diz exatamente o quão forte é essa relação. O problema pode ser corrigido dividindo a covariância pelo desvio padrão para obter o coeficiente de correlação.
Corr(X,Y) = Cov(X,Y) / σXσY
Voltar ao início

> Vantagens do Coeficiente de Correlação

O Coeficiente de Correlação tem várias vantagens sobre covariância para determinar os pontos fortes de relações:

• a covariância pode assumir praticamente qualquer número, enquanto uma correlação é limitada: -1 a + 1.
• por causa de suas limitações numéricas, a correlação é mais útil para determinar o quão forte é a relação entre as duas variáveis.
• a correlação não possui unidades. A covariância sempre tem unidades
• a correlação não é afetada por mudanças no centro (ou seja, média) ou a escala das variáveis

Voltar ao início

Calcular a Covariância no Excel

Assista o vídeo ou siga os passos abaixo (esta é para o Excel 2013, mas os passos são os mesmos para o Excel 2016):

Covariância no Excel: Visão geral

Covariância dá-lhe um número positivo, se as variáveis estão positivamente relacionados. Você receberá um número negativo se eles estiverem relacionados negativamente. Uma alta covariância basicamente indica que há uma forte relação entre as variáveis. Um valor baixo significa que há um relacionamento fraco.

covariância no Excel: passos

Passo 1: Insira seus dados em duas colunas no Excel. Por exemplo, digite seus valores X na coluna A e seus valores Y na coluna B.

Etapa 2: Clique na guia “Dados” e clique em “Análise de dados.”A janela de Análise de dados será aberta.Etapa 3: Escolha “covariância” e clique em ” OK.”

Etapa 4: Clique em “intervalo de entrada” e selecione todos os seus dados. Inclua cabeçalhos de coluna se você os tiver.Etapa 5: Clique na caixa de seleção” etiquetas na primeira linha ” se você incluiu cabeçalhos de coluna em sua seleção de dados.Etapa 6: Selecione “intervalo de saída” e selecione uma área na planilha. Um bom lugar para selecionar é uma área à direita do seu conjunto de dados.

Etapa 7: Clique em ” OK.”A covariância aparecerá na área que você selecionou na Etapa 5.

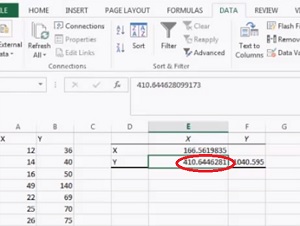
é isso!

dica: execute a função de correlação no Excel depois de executar covariância no Excel 2013. A correlação lhe dará um valor para o relacionamento. 1 é correlação perfeita e 0 não é correlação. Tudo o que você pode realmente dizer da covariância é se há um relacionamento positivo ou negativo.

confira nosso canal no YouTube para obter mais dicas e ajuda do Excel!

voltar ao topo

Dodge, Y. (2008). A enciclopédia concisa de Estatísticas. Springer.Everitt, B. S.; Skrondal, A. (2010), the Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). O Guia de Desenho animado para estatísticas. HarperPerennial.

—————————————————————————

precisa de ajuda com uma lição de casa ou pergunta de teste? Com o Chegg Study, você pode obter soluções passo a passo para suas perguntas de um especialista na área. Seus primeiros 30 minutos com um tutor Chegg são gratuitos!