¿Qué es la Simulación de Monte Carlo?

La simulación de Monte Carlo es un proceso de uso de curvas de probabilidad para determinar la probabilidad de un resultado. Puedes rascarte la cabeza aquí y decir… «Hey Rick, una curva de distribución tiene una matriz de valores. Entonces, ¿cómo determino exactamente la probabilidad de un resultado?»Y mejor aún, cómo lo hago en Microsoft Excel sin ningún complemento especial que nunca preguntarías.Esto se hace ejecutando la simulación miles de veces y analizando la distribución de la salida. Esto es particularmente importante cuando se está analizando la salida de varias curvas de distribución que se alimentan entre sí.Ejemplo:

• # de Unidades vendidas puede tener una curva de distribución
• multiplicada por el precio de mercado, que puede tener otra curva de distribución
• menos salarios variables que tienen otra curva
• etc., sucesivamente.

Una vez que todas estas distribuciones se entremezclan, la salida puede ser bastante compleja. Ejecutar miles de iteraciones (o simulaciones) de estas curvas puede darle algunas ideas. Esto es particularmente útil para analizar el riesgo potencial de una decisión.

Describir Monte Carlo

Al describir la simulación de Monte Carlo, a menudo me refiero a la película de 1980 Juegos de guerra, donde un joven Mathew Broderick (antes de Ferris Bueller) es un hacker que usa su módem telefónico para piratear las computadoras del Pentágono y comenzar la 3ª Guerra Mundial. Algo así. Luego hizo que las computadoras del Pentágono hicieran muchas simulaciones de los juegos Tic Tac Toe para enseñarle a la computadora que nadie va a tener una guerra nuclear, y salvar al mundo en el proceso.Gracias Ferris. Eres un héroe.Aquí tienes un vistazo de la película para mostrarte Montecarlo a lo grande en acción. Asumo que pasarás por alto la política, los abrazos de hombres incómodos y, por supuesto, Dabney Coleman.

Curvas de distribución

Hay varias curvas de distribución que puede usar para configurar su simulación de Monte Carlo. Y estas curvas pueden intercambiarse en función de la variable. Microsoft no tiene una fórmula llamada «Simulación de Monte Carlo» en la barra de menús 🙂

Distribución uniforme

En una distribución uniforme, hay la misma probabilidad en cualquier lugar entre el mínimo y el máximo. Una distribución uniforme parece un rectángulo.

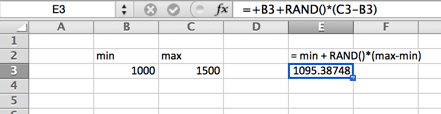
Distribución normal (gaussiana)

Esta es también su curva estándar en forma de campana. Esta Fórmula de simulación de Monte Carlo se caracteriza por estar distribuida uniformemente en cada lado (la mediana y la media son iguales, y no tienen sesgo). Las colas de la curva van hasta el infinito. Por lo tanto, esta puede no ser la curva ideal para los precios de la vivienda, donde unas pocas casas de extremo superior aumentan el promedio (media) muy por encima de la mediana, o en casos en los que hay un mínimo o máximo duro. Un ejemplo de esto puede ser el salario mínimo en su localidad. Tenga en cuenta que el nombre de la función varía según su versión.

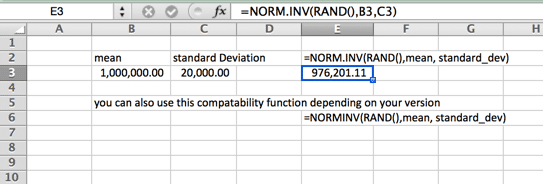
Distribución Lognormal

Una distribución donde el logaritmo se distribuye normalmente con la media y la desviación estándar. Por lo tanto, la configuración es similar a la distribución normal, pero tenga en cuenta que las variables mean y standard_dev están destinadas a representar el logaritmo.

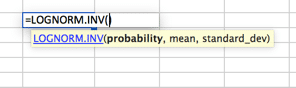
Distribución de Poisson

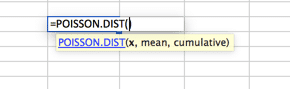
Esta es probablemente la distribución más infrautilizada. De forma predeterminada, muchas personas usan una curva de distribución normal cuando Poisson se adapta mejor a sus modelos. Poisson se describe mejor cuando hay una gran distribución cerca del principio que se disipa rápidamente a una larga cola en un lado. Un ejemplo de esto sería un centro de llamadas, donde no se responden llamadas antes del segundo CERO. Seguido de la mayoría de las llamadas contestadas en los primeros 2 intervalos (digamos 30 y 60 segundos) con una caída rápida de volumen y una cola larga, con muy pocas llamadas contestadas en 20 minutos (supuestamente).

El propósito aquí no es mostrarle todas las distribuciones posibles en Excel, ya que eso está fuera del alcance de este artículo. Más bien para asegurarse de que sabe que hay muchas opciones disponibles para su simulación de Monte Carlo. No caiga en la trampa de suponer que una curva de distribución normal es la adecuada para todo el modelado de datos. Para encontrar más curvas, vaya a las Funciones Estadísticas de su libro de Excel e investigue. Si tienes preguntas, hazlas en la sección de comentarios a continuación.

Construyendo El Modelo

Para esta configuración asumiremos una distribución normal y 1000 iteraciones.

Variables de entrada

La configuración asume una distribución normal. Una distribución normal requiere tres variables: probabilidad, media y desviación estándar. Abordaremos la media y la desviación estándar en nuestro primer paso. Asumo un problema de previsión financiera que consiste en Ingresos, Gastos Variables y Fijos. Donde los Ingresos menos los Gastos Variables menos los Gastos Fijos equivalen a Ganancias. Los gastos fijos son costos hundidos en planta y equipo, por lo que no se asume ninguna curva de distribución. Se asumen curvas de distribución para los Ingresos y los Gastos Variables.

Primera simulación

El siguiente ejemplo indica la configuración de los ingresos. La fórmula se puede copiar y pegar en la celda D6 para gastos variables. Para los ingresos y gastos que la norma de la función.INV() donde los parámetros son:

• Probabilidad = la función RAND () para obtener un número aleatorio basado en los otros criterios dentro de la distribución.
• Media = Media utilizada en el paso 1. Para los ingresos es C3.
• Desviación estándar = La Desviación estándar utilizada en el paso 1. Para los ingresos es C4

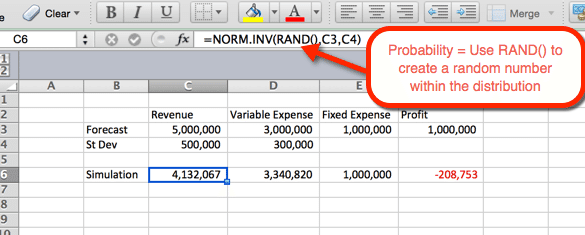
Dado que RAND () se usa como probabilidad, se genera una probabilidad aleatoria en la actualización. Usaremos esto a nuestro favor en el siguiente paso.

1,000 Simulaciones

Hay varias formas de hacer 1.000 o más variaciones. La opción más sencilla es tomar la fórmula del paso #2 y hacerla absoluta. Luego, copie y pegue 1000 veces. Eso es simple, pero no muy elegante. Y si Ferris Bueller puede salvar el mundo mostrando un nuevo juego de Tic Tac Toe a una computadora, entonces también podemos darle vida a este análisis. Aventurémonos en el mundo de las mesas.

• Primero queremos crear un esquema para una tabla. Hacemos esto enumerando los números del 1 al 1000 en filas. En la imagen de ejemplo a continuación, la lista de números comienza en B12.
• en la siguiente columna, en la celda C12, haremos referencia a la primera iteración.

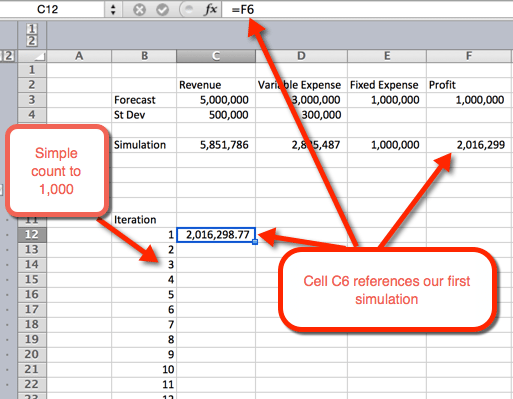
• A continuación, resalte el área donde queremos alojar las 1000 iteraciones
• Seleccionar Datos > Tablas de datos
• Para la celda de entrada de columna: Seleccione una celda en blanco. En el archivo de descarga, se selecciona la celda D11
• Seleccionar Aceptar

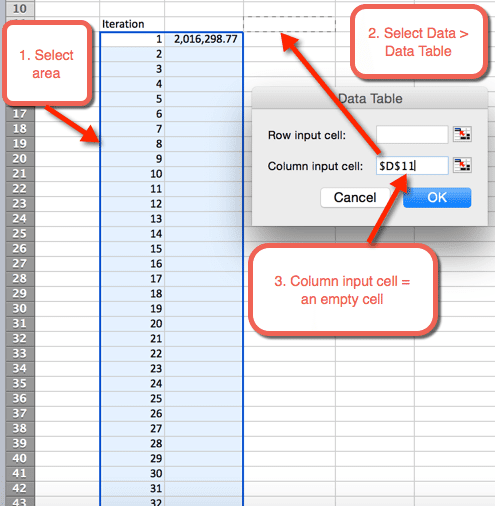
• Una vez seleccionado OK del paso anterior, se inserta una tabla que rellena automáticamente las 1000 simulaciones

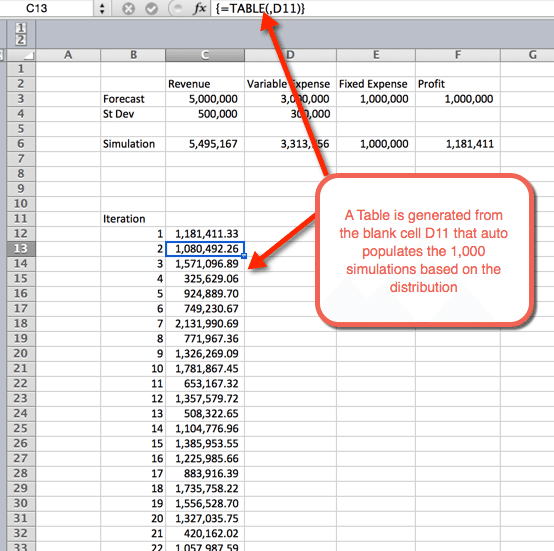
Estadísticas de resumen

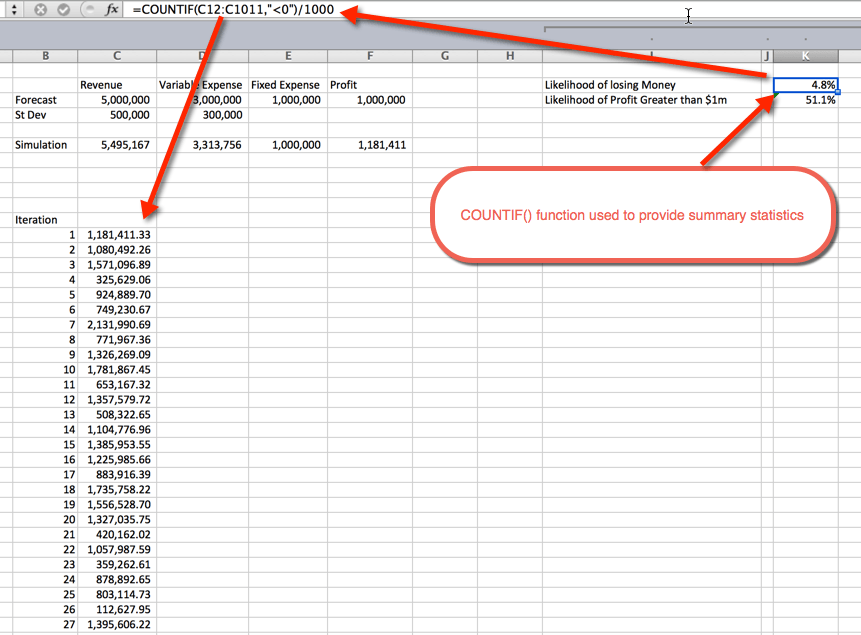
Una vez ejecutadas las simulaciones, es hora de recopilar estadísticas de resumen. Esto se puede hacer de varias maneras. En este ejemplo utilicé la función COUNTIF () para determinar el porcentaje de simulaciones que no son rentables y la probabilidad de un beneficio superior a 1 millón de dólares. Como se esperaba, la probabilidad de más de $1 MILLÓN ronda el 50%. Esto se debe a que usamos curvas de distribución normales que se distribuyen uniformemente alrededor de la media, que era de $1 MILLÓN. La probabilidad de perder dinero es del 4,8%. Esto se recopiló usando la función COUNTIF () para contar las simulaciones que eran inferiores a cero, y dividiendo por las 1.000 iteraciones totales.

Obtenga la descarga

En el video de arriba, Oz pregunta sobre los diversos usos de la Simulación de Monte Carlo. ¿Para qué lo has usado? ¿Hay algún ejemplo específico que puedas compartir con el grupo? Si es así, deje una nota a continuación en la sección de comentarios. Además, no dude en suscribirse a nuestro boletín de noticias, para que pueda mantenerse al día como nuevo Excel.TV se anuncian los espectáculos. Déjame un mensaje a continuación para mantenerme en contacto.