Contenido (Haga clic para ir a esa sección):
- Definición & Fórmula
- Ejemplo
- Problemas con la interpretación
- Ventajas
- Covarianza en Excel
Definición & Fórmula
La covarianza es una medida de cuánto varían juntas dos variables aleatorias. Es similar a la varianza, pero donde la varianza te dice cómo varía una sola variable, la varianza co te dice cómo varían dos variables juntas.
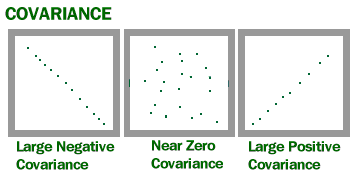
Imagen de U of Wisconsin.
La Fórmula de Covarianza
Vea el video para ver un ejemplo:
¿No puedes ver el video? Haga clic aquí.
La fórmula es:
Cov (X, Y) = Σ E ((X – μ) E ( Y-ν)) / n-1 donde:
- X es una variable aleatoria
- E(X) = µ es el valor esperado (media) de la variable aleatoria X y
- E(Y) = ν es el valor esperado (media) de la variable aleatoria Y
- n = el número de elementos en el conjunto de datos.
- Σ notación sumatoria.
Volver al principio
Ejemplo
Calcular la covarianza para el siguiente conjunto de datos:
x: 2.1, 2.5, 3.6, 4.0 (media = 3.1)
y: 8, 10, 12, 14 (media = 11)
Sustituir los valores en la fórmula y resolver:
Cov(X,Y) = ΣE((X-μ)(Y-ν)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267
El resultado es positivo, lo que significa que las variables están relacionadas positivamente.
Nota sobre la división por n o n-1:
Cuando se trata de muestras, hay términos n-1 que tienen la libertad de variar (ver: Grados de libertad). Si está encontrando la covarianza de solo dos variables aleatorias, divida por n.
Volver al principio
Problemas de interpretación
Una covarianza grande puede significar una relación fuerte entre variables. Sin embargo, no se pueden comparar las variaciones de los conjuntos de datos con diferentes escalas (como libras y pulgadas). Una covarianza débil en un conjunto de datos puede ser fuerte en un conjunto de datos diferente con escalas diferentes.
El principal problema con la interpretación es que la amplia gama de resultados que adquiere hace que sea difícil de interpretar. Por ejemplo, su conjunto de datos podría devolver un valor de 3 o 3000. Esta amplia gama de valores se debe a un simple hecho; Cuanto mayores sean los valores X e Y, mayor será la covarianza. Un valor de 300 nos dice que las variables están correlacionadas, pero a diferencia del coeficiente de correlación, ese número no nos dice exactamente qué tan fuerte es esa relación. El problema se puede solucionar dividiendo la covarianza por la desviación estándar para obtener el coeficiente de correlación.
Corr(X,Y) = Cov(X,Y) / σXσY
Volver al principio
Ventajas del Coeficiente de Correlación
El Coeficiente de Correlación tiene varias ventajas sobre la covarianza para determinar las fortalezas de las relaciones:
- La covarianza puede tomar prácticamente cualquier número, mientras que una correlación es limitada: -1 a +1.
- Debido a sus limitaciones numéricas, la correlación es más útil para determinar qué tan fuerte es la relación entre las dos variables.
- La correlación no tiene unidades. La covarianza siempre tiene unidades
- La correlación no se ve afectada por los cambios en el centro (p. ej. media) o escala de las variables
Volver al principio
Calcular Covarianza en Excel
Vea el video o siga los pasos a continuación (esto es para Excel 2013, pero los pasos son los mismos para Excel 2016):
Covarianza en Excel: Descripción general
La covarianza le da un número positivo si las variables están relacionadas positivamente. Obtendrás un número negativo si están relacionados negativamente. Una alta covarianza indica básicamente que hay una fuerte relación entre las variables. Un valor bajo significa que hay una relación débil.
Covarianza en Excel: Pasos
Paso 1: Ingrese sus datos en dos columnas en Excel. Por ejemplo, escriba sus valores X en la columna A y sus valores Y en la columna B.
Paso 2: Haga clic en la pestaña» Datos «y, a continuación, haga clic en «Análisis de datos».»Se abrirá la ventana de Análisis de Datos.
Paso 3: Elija » Covarianza «y luego haga clic en «ACEPTAR».»
Paso 4: Haga clic en «Rango de entrada» y luego seleccione todos sus datos. Incluya encabezados de columna si los tiene.
Paso 5: Haga clic en la casilla de verificación «Etiquetas en Primera fila» si ha incluido encabezados de columna en su selección de datos.
Paso 6: Seleccione «Rango de salida» y luego seleccione un área en la hoja de trabajo. Un buen lugar para seleccionar es un área justo a la derecha de su conjunto de datos.
Paso 7: Haga clic en «Aceptar».»La covarianza aparecerá en el área seleccionada en el Paso 5.
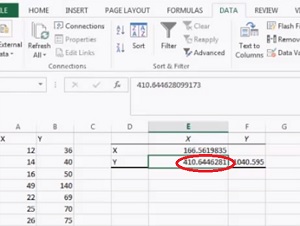
Eso es todo!
Consejo: Ejecute la función de correlación en Excel después de ejecutar la covarianza en Excel 2013. La correlación le dará un valor para la relación. 1 es correlación perfecta y 0 no es correlación. Todo lo que puedes decir de la covarianza es si hay una relación positiva o negativa.
¡Echa un vistazo a nuestro canal de YouTube para obtener más consejos y ayuda de Excel!
Volver al principio
Dodge, Y. (2008). The Concise Encyclopedia of Statistics (en inglés). Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.Gonick, L. (1993). The Cartoon Guide to Statistics (en inglés). HarperPerennial.
Stephanie Glen. «Covariance in Statistics: What is it? Ejemplo» De StatisticsHowTo.com: Estadísticas elementales para el resto de nosotros! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/covariance/
—————————————————————————
¿Necesita ayuda con una pregunta de tarea o examen? Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en el campo. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!