indhold (Klik for at springe til det afsnit):

1. Definition & formel
2. eksempel
3. problemer med fortolkning
4. fordele
5. kovarians i udmærke

Definition& formel

kovarians er et mål for, hvor meget to tilfældige variabler varierer sammen. Det ligner varians, men hvor varians fortæller dig, hvordan en enkelt variabel varierer, Co varians fortæller dig, hvordan to variabler varierer sammen.

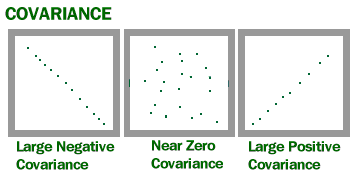
billede fra U.

Kovariansformlen

se videoen for et eksempel:

kan du ikke se videoen? Klik her.

formlen er:
Cov (H,Y) = H E ((H-H) E (Y-H)) / n-1 Hvor:

• H er en tilfældig variabel
• E(H) = L er den forventede værdi (middelværdien) for den tilfældige variabel H og
• E(Y) = L er den forventede værdi (middelværdien) for den tilfældige variabel Y
• n = antallet af elementer i datasættet.
• list summation notation.

tilbage til toppen

eksempel

Beregn kovarians for følgende datasæt:
*: 2.1, 2.5, 3.6, 4.0 (middel = 3.1)
y: 8, 10, 12, 14 (middel = 11)

Erstat værdierne i formlen og løs:
kov(k,y) = kov((k-k)(y-k)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267

resultatet er positivt, hvilket betyder, at variablerne er positivt relaterede.

Bemærk om opdeling med n eller n-1:
når der beskæftiger sig med prøver, er der n-1-udtryk, der har friheden til at variere (se: frihedsgrader). Hvis du finder kovariansen af kun to tilfældige variabler, skal du bare dele med n.
tilbage til toppen

problemer med fortolkning

en stor kovarians kan betyde et stærkt forhold mellem variabler. Du kan dog ikke sammenligne afvigelser over datasæt med forskellige skalaer (som pund og tommer). En svag kovarians i et datasæt kan være en stærk i et andet datasæt med forskellige skalaer.

hovedproblemet med fortolkning er, at den brede vifte af resultater, det tager på, gør det svært at fortolke. For eksempel kan dit datasæt returnere en værdi på 3 eller 3.000. Denne brede vifte af værdier skyldes en simpel kendsgerning; Jo større Y-og Y-værdierne er, desto større er kovariansen. En værdi på 300 fortæller os, at variablerne er korrelerede, men i modsætning til korrelationskoefficienten fortæller dette tal os ikke nøjagtigt, hvor stærkt dette forhold er. Problemet kan løses ved at dividere kovariansen med standardafvigelsen for at få korrelationskoefficienten.
Corr(H,Y) = Cov(H,Y) / kov (h, Y) / tilbage til toppen

fordele ved korrelationskoefficienten

korrelationskoefficienten har flere fordele i forhold til kovarians til bestemmelse af styrker af relationer:

• kovarians kan påtage sig praktisk talt ethvert tal, mens en korrelation er begrænset: -1 til +1.
• på grund af dets numeriske begrænsninger er korrelation mere nyttig til at bestemme, hvor stærk forholdet er mellem de to variabler.
• korrelation har ikke enheder. Kovarians har altid enheder
• korrelation påvirkes ikke af ændringer i midten (dvs.

tilbage til toppen

Beregn kovarians

se videoen, eller følg nedenstående trin (Dette er for 2013, men trinene er de samme for 2013 2016):

oversigt

kovarians giver dig et positivt tal, hvis variablerne er positivt relaterede. Du får et negativt tal, hvis de er negativt relaterede. En høj kovarians indikerer dybest set, at der er et stærkt forhold mellem variablerne. En lav værdi betyder, at der er et svagt forhold.

kovarians i kovarians: trin

Trin 1: Indtast dine data i to kolonner. I kolonne A og dine y-værdier i kolonne B.

Trin 2: Klik på fanen “Data”, og klik derefter på “dataanalyse.”Dataanalysevinduet åbnes.

Trin 3: Vælg “kovarians” og klik derefter på “OK.”

Trin 4: Klik på “Input Range” og vælg derefter alle dine data. Medtag kolonneoverskrifter, hvis du har dem.

Trin 5: Klik på afkrydsningsfeltet “etiketter i første række”, hvis du har inkluderet kolonneoverskrifter i dit datavalg.

Trin 6: Vælg “outputområde”, og vælg derefter et område på regnearket. Et godt sted at vælge er et område lige til højre for dit datasæt.

Trin 7: Klik på “OK.”Kovariansen vises i det område, du valgte i Trin 5.

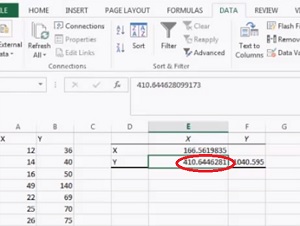
sådan!

Tip: Kør korrelationsfunktionen i udmærke sig, når du har kørt kovarians i udmærke sig 2013. Korrelation vil give dig en værdi for forholdet. 1 er perfekt korrelation og 0 er ingen korrelation. Alt hvad du virkelig kan fortælle fra kovarians er, om der er et positivt eller negativt forhold.

se vores YouTube-kanal for at få flere tips og hjælp!

tilbage til toppen

Dodge, Y. (2008). Den koncise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). Den tegneserie Guide til statistik. HarperPerennial.

—————————————————————————

brug for hjælp til et hjemmearbejde eller test spørgsmål? Med Chegg Study kan du få trinvise løsninger på dine spørgsmål fra en ekspert på området. Dine første 30 minutter med en Chegg tutor er gratis!