co je simulace Monte Carlo?

simulace Monte Carlo je proces použití křivek pravděpodobnosti k určení pravděpodobnosti výsledku. Tady se můžete poškrábat na hlavě a říct… „Ahoj Ricku, distribuční křivka má řadu hodnot. Jak přesně tedy určím pravděpodobnost výsledku?“A ještě lépe, jak to udělat v aplikaci Microsoft Excel bez zvláštního doplňkumyšlenka, kterou byste se nikdy neptali.To se provádí spuštěním simulace tisíckrát a analýzou distribuce výstupu. To je zvláště důležité, když analyzujete výstup několika distribučních křivek, které se navzájem živí.Příklad:

• # prodaných jednotek může mít distribuční křivku
• vynásobenou tržní cenou, která může mít jinou distribuční křivku
• minus variabilní mzdy, které mají jinou křivku
• atd., atd.

jakmile jsou všechny tyto distribuce vzájemně propojeny, výstup může být poměrně složitý. Spuštění tisíců iterací (nebo simulací) těchto křivek vám může poskytnout určité poznatky. To je zvláště užitečné při analýze potenciálního rizika pro rozhodnutí.

popište Monte Carlo

když popisuji simulaci Monte Carlo, často odkazuji na filmové Válečné hry z roku 1980, kde mladý Mathew Broderick (před Ferrisem Buellerem) je hacker, který používá svůj vytáčený modem k hackování do počítačů Pentagonu a zahájení 3. světové války. Tak trochu. Poté nechal počítače Pentagonu provést mnoho simulací her Tic Tac Toe, aby naučil počítač, že nikdo nebude jadernou válku-a zachránit svět v tomto procesu.Díky, Ferrisi. Jsi hrdina.Zde je pohled na film, který vám ukáže velký čas Monte Carlo V Akci. Předpokládám, že přehlédnete politiku, trapný muž objímající a samozřejmě, Dabney Coleman.

distribuční křivky

existují různé distribuční křivky, které můžete použít k nastavení simulace Monte Carlo. A tyto křivky mohou být zaměněny na základě proměnné. Microsoft nemá vzorec nazvaný „Do Monte Carlo Simulation“ v panelu nabídek:)

rovnoměrné rozdělení

v rovnoměrném rozdělení existuje stejná pravděpodobnost kdekoli mezi minimem a maximem. Rovnoměrné rozložení vypadá jako obdélník.

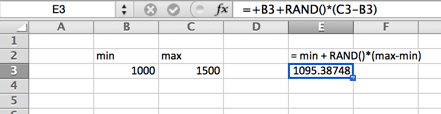
normální (Gaussovské) rozdělení

Toto je také vaše standardní křivka ve tvaru zvonu. Tento simulační vzorec Monte Carlo se vyznačuje tím, že je rovnoměrně rozložen na každé straně(medián a průměr jsou stejné – a žádná šikmost). Ocasy křivky pokračují do nekonečna. To tedy nemusí být ideální křivka pro ceny domů, kde několik špičkových domů zvyšuje průměr (průměr) výrazně nad medián, nebo v případech, kdy existuje tvrdé minimum nebo maximum. Příkladem může být minimální mzda ve vaší lokalitě. Vezměte prosím na vědomí, že název funkce se liší v závislosti na vaší verzi.

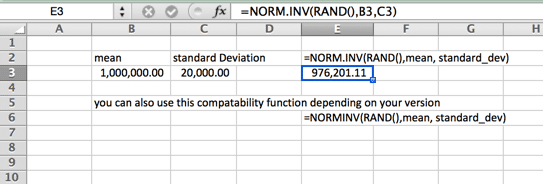
Lognormální rozdělení

rozdělení, kde je logaritmus normálně distribuován se střední a směrodatnou odchylkou. Nastavení je tedy podobné normálnímu rozdělení, ale mějte na paměti, že proměnné mean a standard_dev mají reprezentovat logaritmus.

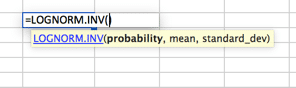
Poissonovo rozdělení

toto je pravděpodobně nejvíce nevyužité rozdělení. Ve výchozím nastavení mnoho lidí používá normální distribuční křivku, když je Poisson vhodnější pro jejich modely. Poisson je nejlépe popsán, když je na samém začátku velká distribuce, která se rychle rozptýlí na dlouhý ocas na jedné straně. Příkladem toho by bylo call centrum, kde před druhou nulou nejsou přijímány žádné hovory. Následuje většina hovorů přijatých v prvních intervalech 2 (řekněme 30 a 60 sekund) s rychlým poklesem hlasitosti a dlouhým ocasem, s velmi malým počtem hovorů přijatých za 20 minut (údajně).

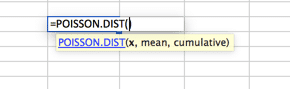
účelem zde není ukázat vám všechny možné distribuce v aplikaci Excel, protože to je mimo rozsah tohoto článku. Spíše se ujistěte, že víte, že pro vaši simulaci Monte Carlo je k dispozici mnoho možností. Nespadají do pasti za předpokladu, že normální distribuční křivka je vhodná pro všechny vaše datové modelování. Chcete-li najít další křivky, přejděte na statistické funkce v sešitu aplikace Excel a prozkoumejte. Máte-li dotazy, vložte je do sekce komentářů níže.

sestavení modelu

pro toto nastavení předpokládáme normální rozdělení a 1 000 iterací.

vstupní proměnné

nastavení předpokládá normální rozdělení. Normální rozdělení vyžaduje tři proměnné; pravděpodobnost, průměr a směrodatná odchylka. V našem prvním kroku se budeme zabývat střední a směrodatnou odchylkou. Předpokládám problém prognózování financí, který se skládá z příjmů, variabilních a fixních výdajů. Kde příjmy minus variabilní náklady minus fixní náklady se rovná zisku. Fixní náklady jsou potopené náklady na zařízení a zařízení, takže se nepředpokládá žádná distribuční křivka. Distribuční křivky se předpokládají pro příjmy a variabilní náklady.

první simulace

níže uvedený příklad označuje nastavení výnosů. Vzorec lze zkopírovat a vložit do buňky D6 pro variabilní náklady. Pro příjmy a výdaje jsme vám funkci normu.INV (), kde jsou parametry:

• Pravděpodobnost = funkce RAND () pro vyvolání náhodného čísla na základě dalších kritérií v rámci distribuce.
• průměr = průměr použitý v kroku 1. Pro příjmy je to C3.
• směrodatná odchylka = směrodatná odchylka použitá v kroku 1. Pro příjmy je to C4

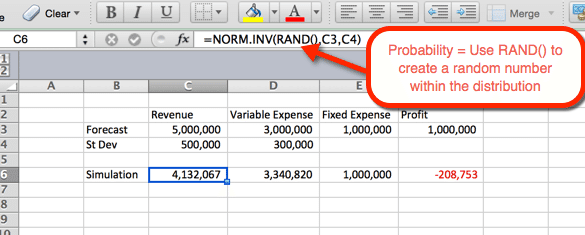
protože RAND() se používá jako pravděpodobnost, náhodná pravděpodobnost je generována při obnovení. Využijeme to v náš prospěch v dalším kroku.

1 000 simulací

existuje několik způsobů, jak provést 1 000 nebo více variací. Nejjednodušší možností je vzít vzorec z kroku č. 2 a učinit jej absolutním. Poté zkopírujte a vložte 1 000krát. To je jednoduché, ale ne moc efektní. A pokud Ferris Bueller dokáže zachránit svět tím, že ukáže novou hru Tic Tac Toe počítači, pak můžeme tuto analýzu také okořenit. Pojďme se pustit do světa stolů.

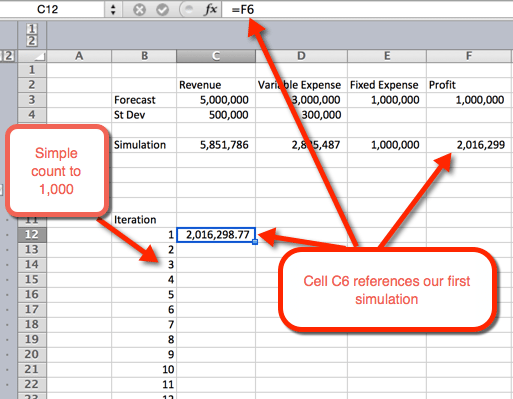
• nejprve chceme vytvořit obrys tabulky. Děláme to tak, že v řádcích uvedeme čísla 1 až 1 000. Na příkladu obrázku níže začíná seznam čísel v B12.
• v dalším sloupci v buňce C12 odkazujeme na první iteraci.

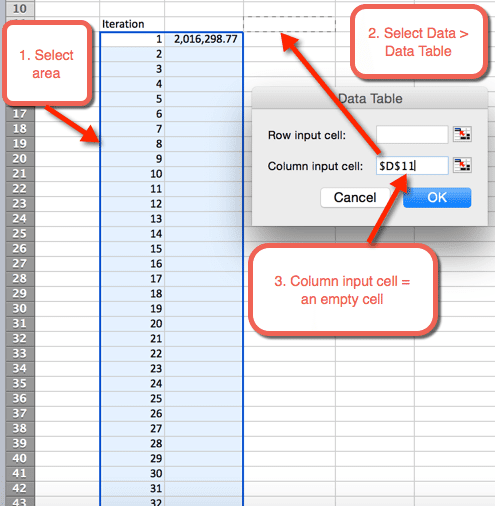
• dále zvýrazněte oblast, kde chceme umístit 1 000 iterací
• vyberte Data > datové tabulky
• pro sloupec Vstupní buňka: vyberte prázdnou buňku. V souboru ke stažení je vybrána buňka D11
• vyberte OK

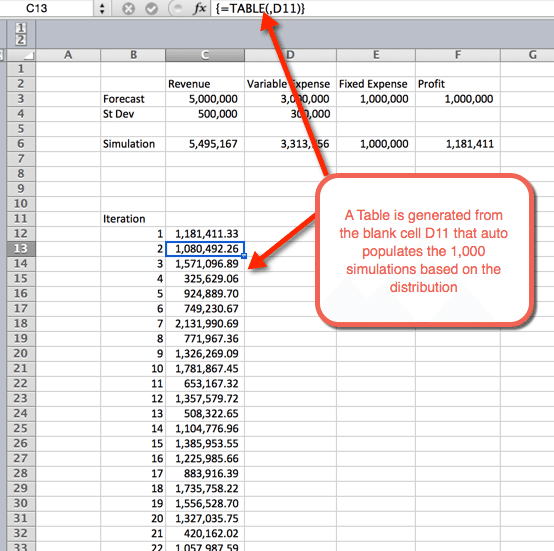
• jakmile je OK vybrán z předchozího kroku, je vložena tabulka, která autopopuluje 1000 simulací

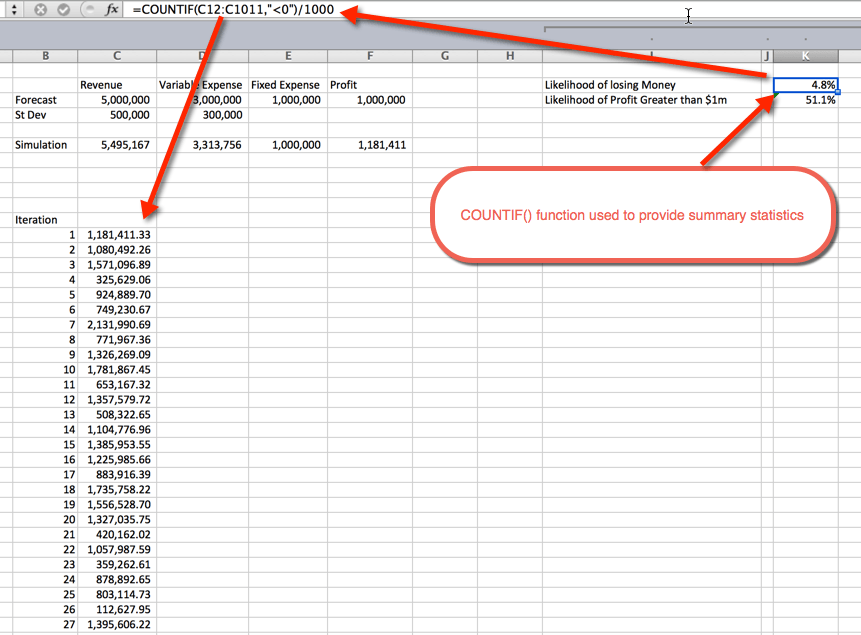
souhrnné statistiky

po spuštění simulací je čas shromáždit souhrnné statistiky. To lze provést několika způsoby. V tomto příkladu jsem použil funkci COUNTIF () k určení procenta simulací, které jsou nerentabilní, a pravděpodobnosti zisku většího než 1 milion dolarů. Jak se dalo očekávat, pravděpodobnost větší než $ 1M se pohybuje kolem 50%. Je to proto, že jsme použili normální distribuční křivky, které jsou rovnoměrně rozloženy kolem průměru ,což bylo $ 1M. pravděpodobnost ztráty peněz je 4,8%. Toto bylo shromážděno pomocí funkce COUNTIF () pro počítání simulací, které byly menší než nula, a vydělením 1000 celkových iterací.

získejte stažení

ve videu výše se Oz ptá na různá použití pro simulaci Monte Carlo. Na co jsi ho použil? Existují nějaké konkrétní příklady, které můžete sdílet se skupinou? Pokud ano, zanechte poznámku níže v sekci komentáře. Taky, neváhejte se přihlásit k odběru novinek, takže můžete zůstat až do dnešního dne jako nový Excel.TV přehlídky jsou vyhlášeny. Zanechte mi zprávu níže, abyste zůstali v kontaktu.