obsah (kliknutím přeskočíte na tuto sekci):

1. definice & vzorec
2. příklad
3. problémy s interpretací
4. výhody
5. kovariance v Excelu

definice & vzorec

kovariance je měřítkem toho, jak moc se dvě náhodné proměnné mění dohromady. Je to podobné rozptylu, ale tam, kde vám rozptyl říká, jak se mění jedna proměnná, rozptyl co vám říká, jak se dvě proměnné liší společně.

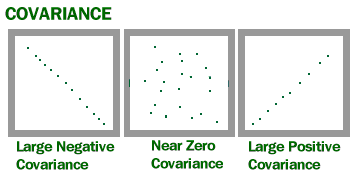
obrázek z U Wisconsinu.

vzorec kovariance

podívejte se na video:

nevidíte to video? Kliknout.

vzorec je:
Cov (X,Y) = Σ E ((X-μ) E (Y-ν)) / n-1 Kde:

• X je náhodná proměnná
• E (X) = μ je očekávaná hodnota (průměr) náhodné proměnné X a
• E (Y) = ν je očekávaná hodnota (průměr) náhodné proměnné Y
• n = počet položek v datové sadě.
• Σ součet notace.

zpět nahoru

příklad

Vypočítejte kovarianci pro následující datovou sadu:
x: 2.1, 2.5, 3.6, 4.0 (mean = 3.1)
y: 8, 10, 12, 14 (mean = 11)

nahraďte hodnoty do vzorce a vyřešte:
Cov(X,Y) = ΣE((X-μ) (Y-ν)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267

výsledek je pozitivní, což znamená, že proměnné jsou pozitivně příbuzné.

poznámka k dělení n nebo n-1:
při práci se vzorky existují pojmy n-1, které mají volnost měnit (viz: stupně volnosti). Pokud nacházíte kovarianci pouze dvou náhodných proměnných, vydělte n.
zpět na začátek

problémy s interpretací

velká kovariance může znamenat silný vztah mezi proměnnými. Nelze však porovnávat odchylky v datových sadách s různými měřítky (například libry a palce). Slabá kovariance v jedné datové sadě může být silná v jiné datové sadě s různými měřítky.

hlavním problémem interpretace je, že široká škála výsledků, které přijímá, ztěžuje interpretaci. Například vaše datová sada může vrátit hodnotu 3 nebo 3 000. Tento široký rozsah hodnot je způsoben jednoduchým faktem; Čím větší jsou hodnoty X a Y, tím větší je kovariance. Hodnota 300 nám říká, že proměnné jsou korelovány, ale na rozdíl od korelačního koeficientu nám toto číslo neříká přesně, jak silný je tento vztah. Problém lze vyřešit vydělením kovariance směrodatnou odchylkou, aby se získal korelační koeficient.
Corr (X, Y) = Cov (X,Y) / σXσY
zpět nahoru

výhody korelačního koeficientu

korelační koeficient má několik výhod oproti kovarianci pro stanovení silných vztahů:

• kovariance může mít prakticky libovolné číslo, zatímco korelace je omezená: -1 až +1.
• vzhledem k numerickým omezením je korelace užitečnější pro určení, jak silný je vztah mezi těmito dvěma proměnnými.
• korelace nemá jednotky. Kovariance má vždy jednotky
• korelace není ovlivněna změnami ve středu (tj.

zpět nahoru

Vypočítejte kovarianci v aplikaci Excel

podívejte se na video nebo postupujte podle níže uvedených kroků(toto je pro Excel 2013, ale kroky jsou stejné pro Excel 2016):

kovariance v Excelu: přehled

kovariance vám dává kladné číslo, pokud jsou proměnné pozitivně příbuzné. Dostanete záporné číslo, pokud jsou negativně příbuzné. Vysoká kovariance v podstatě naznačuje, že mezi proměnnými existuje silný vztah. Nízká hodnota znamená, že existuje slabý vztah.

kovariance v aplikaci Excel: kroky

Krok 1: Zadejte data do dvou sloupců v aplikaci Excel. Například zadejte hodnoty X do sloupce A a hodnoty Y do sloupce B.

Krok 2: Klikněte na kartu“ Data „a poté na“ Analýza dat.“Otevře se okno pro analýzu dat.

Krok 3: Zvolte „kovariance“ a poté klikněte na “ OK.“

Krok 4: Klikněte na „rozsah vstupu“ a poté vyberte všechna data. Zahrnout záhlaví sloupců, pokud je máte.

Krok 5: zaškrtněte políčko“ Štítky v prvním řádku“, pokud jste do výběru dat zahrnuli záhlaví sloupců.

Krok 6: Vyberte „výstupní rozsah“ a poté vyberte oblast v listu. Dobrým místem pro výběr je oblast napravo od datové sady.

Krok 7: Klikněte na “ OK.“Kovariance se objeví v oblasti, kterou jste vybrali v kroku 5.

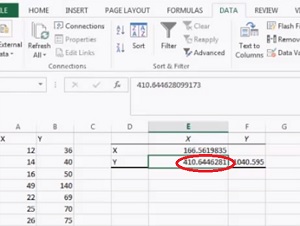
to je ono!

Tip: Po spuštění kovariance v aplikaci Excel 2013 spusťte korelační funkci v aplikaci Excel. Korelace vám dá hodnotu vztahu. 1 je dokonalá korelace a 0 není korelace. Z kovariance můžete opravdu říct, zda existuje pozitivní nebo negativní vztah.

podívejte se na náš YouTube kanál pro více Excel tipy a pomoc!

zpět na začátek

Dodge, y. (2008). Stručná encyklopedie statistik. Springere.
Everitt, B. S.; Skrondal, a. (2010), Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). Kreslený průvodce statistikami. HarperPerennial.

—————————————————————————

potřebujete pomoc s domácími úkoly nebo testovací otázkou? S Chegg Study, můžete získat krok za krokem řešení vašich otázek od odborníka v oboru. Váš první 30 minut s Chegg tutorem je zdarma!