cuprins (Click pentru a trece la acea secțiune):

1. definiție & formulă
2. exemplu
3. probleme cu interpretarea
4. avantaje
5. covarianță în Excel

definiție & formulă

covarianța este o măsură a cât de mult variază două variabile aleatorii împreună. Este similar cu varianța, dar unde varianța vă spune cum variază o singură variabilă, varianța co vă spune cum variază două variabile împreună.

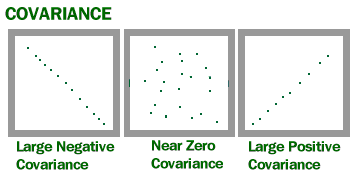
imagine din U din Wisconsin.

formula de covarianță

Urmăriți videoclipul pentru un exemplu:

nu se poate vedea video? Click aici.

formula este:
Cov (X,Y) = inkt(X – inkt) E (Y-inkt)) / n-1 unde:

• X este o variabilă aleatorie
• E(X) = ecuot este valoarea așteptată (media) a variabilei aleatorii X și
• E(Y) = ecuot este valoarea așteptată (media) a variabilei aleatorii Y
• n = numărul de itemi din setul de date.
• notație de însumare a cifrelor.

înapoi la început

exemplu

calculați covarianța pentru următorul set de date:
x: 2.1, 2.5, 3.6, 4.0 (medie = 3.1)
y: 8, 10, 12, 14 (medie = 11)

înlocuiți valorile în formulă și rezolvați:
COV(x,y) = NOx((x-NOx)(y-NOx)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267

rezultatul este pozitiv, ceea ce înseamnă că variabilele sunt legate pozitiv.

notă privind împărțirea la n sau n-1:
atunci când se ocupă de eșantioane, există termeni n-1 care au libertatea de a varia (Vezi: grade de libertate). Dacă găsiți covarianța a doar două variabile aleatorii, împărțiți doar la n.
înapoi la început

probleme de interpretare

o covarianță mare poate însemna o relație puternică între variabile. Cu toate acestea, nu puteți compara variațiile peste seturile de date cu scale diferite (cum ar fi lire sterline și inci). O covarianță slabă într-un set de date poate fi una puternică într-un set de date diferit, cu scale diferite.

principala problemă cu interpretarea este că gama largă de rezultate pe care le preia face dificilă interpretarea. De exemplu, setul dvs. de date ar putea returna o valoare de 3 sau 3.000. Această gamă largă de valori este cauzată de un simplu fapt; Cu cât valorile X și Y sunt mai mari, cu atât este mai mare covarianța. O valoare de 300 ne spune că variabilele sunt corelate, dar spre deosebire de coeficientul de corelație, acel număr nu ne spune exact cât de puternică este acea relație. Problema poate fi rezolvată prin împărțirea covarianței la abaterea standard pentru a obține coeficientul de corelație.
Corr ( X,Y) = COV (X,Y) / olxx olxy
înapoi la început

avantajele coeficientului de corelație

coeficientul de corelație are mai multe avantaje față de covarianță pentru determinarea punctelor forte ale relațiilor:

• covarianța poate prelua practic orice număr în timp ce o corelație este limitată: -1 la +1.
• din cauza limitărilor numerice, corelația este mai utilă pentru a determina cât de puternică este relația dintre cele două variabile.
• corelația nu are unități. Covarianța are întotdeauna unități
• corelația nu este afectată de schimbările din centru (adică. medie) sau scara variabilelor

înapoi la început

calculați covarianța în Excel

Urmăriți videoclipul sau urmați pașii de mai jos (aceasta este pentru Excel 2013, dar pașii sunt aceiași pentru Excel 2016):

covarianța în Excel: Prezentare generală

covarianța vă oferă un număr pozitiv dacă variabilele sunt legate pozitiv. Veți obține un număr negativ dacă acestea sunt legate negativ. O covarianță ridicată indică practic că există o relație puternică între variabile. O valoare scăzută înseamnă că există o relație slabă.

covarianță în Excel: pași

Pasul 1: Introduceți datele în două coloane în Excel. De exemplu, tastați valorile X în coloana A și valorile Y în coloana B.

Pasul 2: Faceți clic pe fila „Date” și apoi faceți clic pe „analiza datelor.”Se va deschide fereastra de analiză a datelor.

Pasul 3: Alegeți „covarianță” și apoi faceți clic pe „OK.”

Pasul 4: Faceți clic pe” interval de intrare ” și apoi selectați toate datele. Includeți anteturi de coloană dacă le aveți.

Pasul 5: Faceți clic pe caseta de selectare „etichete în primul rând” dacă ați inclus anteturi de coloană în selecția de date.

Pasul 6: Selectați „interval de ieșire” și apoi selectați o zonă din foaia de lucru. Un loc bun pentru a selecta este o zonă chiar în dreapta setului dvs. de date.

Pasul 7: Faceți clic pe „OK.”Covarianța va apărea în zona selectată la Pasul 5.

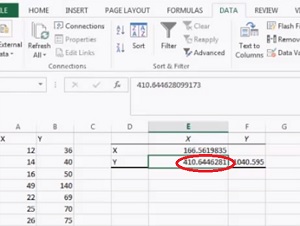
asta e!

sfat: rulați funcția de corelare în Excel după ce executați covarianță în Excel 2013. Corelația vă va oferi o valoare pentru relație. 1 este corelație perfectă și 0 este nici o corelație. Tot ce puteți spune cu adevărat din covarianță este dacă există o relație pozitivă sau negativă.

consultați canalul nostru YouTube pentru mai multe sfaturi și ajutor Excel!

Înapoi sus

Dodge, Y. (2008). Enciclopedia concisă a statisticilor. Springer.
Everitt, B. S.; Skrondal, A. (2010), dicționarul de Statistică Cambridge, Cambridge University Press.
Gonick, L. (1993). Ghidul de desene animate pentru statistici. HarperPerennial.

—————————————————————————

aveți nevoie de ajutor cu o temă sau o întrebare de testare? Cu studiul Chegg, puteți obține soluții pas cu pas la întrebările dvs. de la un expert în domeniu. Primele 30 de minute cu un tutore Chegg sunt gratuite!